题目内容
【题目】如图1,AB为半圆O的直径,半径OP⊥AB,过劣弧AP上一点D作DC⊥AB于点C.连接DB,交OP于点E,∠DBA=22.5°.
⑴ 若OC=2,则AC的长为 ;
⑵ 试写出AC与PE之间的数量关系,并说明理由;
⑶ 连接AD并延长,交OP的延长线于点G,设DC=x,GP=y,请求出x与y之间的等量关系式. (请先补全图形,再解答)
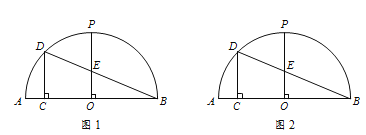
【答案】⑴ ![]() ;⑵ 见解析;⑶ y=
;⑵ 见解析;⑶ y=![]()
【解析】
(1)如图,连接OD,则有∠AOD=45°,所以△DOC为等腰直角三角形,又OC=2,所以DO=AO=2![]() ,故可求出AC的长;
,故可求出AC的长;
(2)连接AD,DP,过点D作DF⊥OP,垂足为点F. 证AC=PF或AC=EF ,证DP=DE
证PF=EF=![]() ,故可证出PE=2AC ;
,故可证出PE=2AC ;
(3)首先求出![]() ,再求AB=
,再求AB=![]() ,再证△DGE≌△DBA,得GE=AB=
,再证△DGE≌△DBA,得GE=AB=![]() ,由PE=2AC得PE=2
,由PE=2AC得PE=2![]() ,再根据GP=GE-PE可求结论.
,再根据GP=GE-PE可求结论.
(1)连接OD,如图,
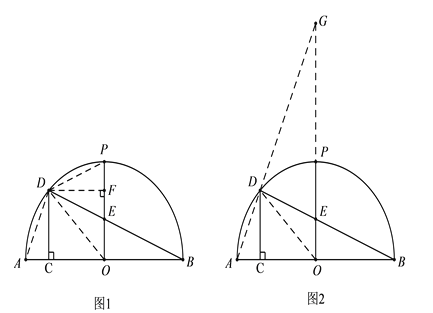
∵∠B=22.5°,
∴∠DOC=45°,
∵DC⊥AB
∴△DOC为等腰直角三角形,
∵OC=2,
∴OD=2![]() ,
,
∴AO=2![]() ,
,
∴AC=AO-OC=![]() .
.
⑵ 连接AD,DP,过点D作DF⊥OP,垂足为点F.
∵OP⊥AB,
∴∠POD=∠DOC=45°,
∴AD=PD,
∵△DOC为等腰直角三角形,
∴DC=CO,
易证DF=CO,
∴DC=DF,
∴Rt△DAC≌Rt△DPF,
∴PF=AC,
∵DO=AO,∠DOA=45°
∴∠DAC=67.5°
∴∠DPE=67.5°,
∵OD=OB,∠B=22.5°,
∴∠ODE=22.5°
∴∠DEP=22.5°+45°=67.5°
∴∠DEP=∠DPE
∴PF=EF=![]()
∴PE=2AC
(3)如图2,由∠DCO=90°,∠DOC=45°得![]()
∴ AB=2OD=![]()
∵AB是直径,
∴∠ADB=∠EDG=90°,
由(2)得AD=ED,∠DEG=∠DAC
∴△DGE≌△DBA
∴ GE=AB=![]()
∵ PE=2AC
∴ PE=2![]()
∴ GP=GE-PE=![]()
即:y=![]()