Question

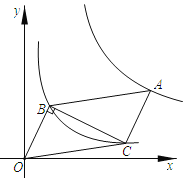
【题目】如图，在平面直角坐标系中，平行四边形ABOC的顶点B，C在反比例函数y=(x>O)的图象上，点A在反比例函数y=(k>O)的图象上，若点B的坐标为(1，2)，∠OBC=90°,则k的值为( )

A. B.3 C.5 D.12.5

Answer 1

【答案】D

【解析】

先由点B的坐标得出m的值，再结合∠OBC=90°求出点C的坐标，进而结合平行四边形的对角线互相平分得出点A的坐标，代入即可求出k的值．

过点B作BH⊥x轴于点H，过点C作CM⊥BH于点M，过点A作AN⊥MC于点N交MC的延长线于点N，

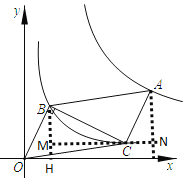
∵点B(1，2)，

∴OH=1，BH=2，

∴∠OHB=∠BMC=∠ANC=90°，

∵平行四边形ABOC，∠OBC=90°，

∴OB=AC，OB∥AC，

∴∠ACB=90°，

∴∠OBH+∠HBC=90°，∠HBC+∠MCB=90°，∠MCB+∠ACN=90°，

∴∠OBH=∠MCB=∠CAN，

在△OBH和△CAN中，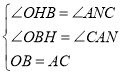

△OBH≌△CAN(AAS)

∴BH=AN=2，OH=CN=1，

∵点B(1,2)在反比例函数y=上，

∴m=1×2=2，

∴y=，

设点C(n，)则点A(n+1，+2)，

∴BM=2-， MC=n-1，

∵∠OBH=∠MCB，∠OHB=∠BMC，

∴△OBH∽△BMC，

∴， 即，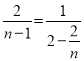

解之：n1=4，n2=1(舍去)，

∴n+1=5，+2=，

∴点A(5，)，

∵点A在反比例函数y=上，

∴k=5×=，

故选D