Question

【题目】如图，在等腰Rt△ABC中，∠BAC＝90°，BC＝2，点P是△ABC内部的一个动点，且满足∠PBC＝∠PCA，则线段AP长的最小值为（　　）

A.0.5B.﹣1C.2﹣D.

Answer 1

【答案】C

【解析】

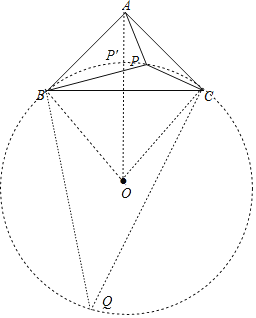
先计算出∠PBC+∠PCB＝45°，则∠BPC＝135°，利用圆周角定理可判断点P在以BC为弦的⊙O上，如图，连接OA交于P′，作所对的圆周角∠BQC，利用圆周角定理计算出∠BOC＝90°，从而得到△OBC为等腰直角三角形，四边形ABOC为正方形，所以OA＝BC＝2，OB=，根据三角形三边关系得到AP≥OA﹣OP（当且仅当A、P、O共线时取等号，即P点在P′位置），于是得到AP的最小值.

解：∵△ABC为等腰直角三角形，

∴∠ACB＝45°，即∠PCB+∠PCA＝45°，

∵∠PBC＝∠PCA，

∴∠PBC+∠PCB＝45°，

∴∠BPC＝135°，

∴点P在以BC为弦的⊙O上，如图，连接OA交于P′，

作所对的圆周角∠BQC，则∠BCQ＝180°﹣∠BPC＝45°，

∴∠BOC＝2∠BQC＝90°，

∴△OBC为等腰直角三角形，

∴四边形ABOC为正方形，

∴OA＝BC＝2，

∴OB＝BC＝，

∵AP≥OA﹣OP（当且仅当A、P、O共线时取等号，即P点在P′位置），

∴AP的最小值为2﹣．

故选：C．