题目内容
【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
【答案】解:由题意可知∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
过点B作BE⊥AD,垂足为E,如图所示: 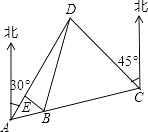
由题意可知∠DAC=75°﹣30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60° BD=BC=CD=20km,
∴∠ADB=∠DBC﹣∠DAC=15°,
∴BE=sin15°BD≈0.25×20≈5m,
∴AB= ![]() =
= ![]() ≈7m,
≈7m,
∴AB+BC+CD≈7+20+20≈47m.
答:从A地跑到D地的路程约为47m.
【解析】解直角三角形的基本方法是把已知角放在直角三角形中,因此需过B作垂线构造直角三角形,由三角函数可求出BE,再由BE求出AB, 进而求出整个路程.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:![]() 总利润
总利润![]() 单件利润
单件利润![]() 销售量
销售量![]()
商品价格 | A | B |
进价 | 1200 | 1000 |
售价 | 1350 | 1200 |
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原进价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原售价销售,而B商品按原售价打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?




