题目内容
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA,OB的长和经过点A,B,C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
【答案】
(1)解:设OA的长为x,则OB=5﹣x;
∵OC=2,AB=5,∠BOC=∠AOC=90°,∠OAC=∠OCB;
∴△AOC∽△COB,∴OC2=OAOB
∴22=x(5﹣x)
解得:x1=1,x2=4,
∵OA<OB,∴OA=1,OB=4;
∴点A、B、C的坐标分别是:A(﹣1,0),B(4,0),C(0,2);
方法一:设经过点A、B、C的抛物线的关系式为:y=ax2+bx+2,
将A、B、C三点的坐标代入得 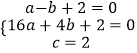
解得:a= ![]() ,b=
,b= ![]() ,c=2
,c=2
所以这个二次函数的表达式为: ![]()
方法二:设过点A、B、C的抛物线的关系式为:y=a(x+1)(x﹣4)
将C点的坐标代入得:a= ![]()
所以这个二次函数的表达式为: ![]()
(2)解:①当△BDE是等腰三角形时,点E的坐标分别是: ![]() ,
, ![]() ,
, ![]() .
.
②如图1,连接OP,
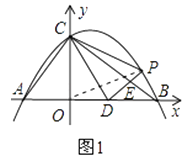
S△CDP=S四边形CODP﹣S△COD=S△COP+S△ODP﹣S△COD
= ![]() =m+n﹣2
=m+n﹣2
= ![]() =
= ![]()
∴当m= ![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为( ![]() ,
, ![]() ),
),
S△CDP的最大值是 ![]() .
.
另解:如图2、图3,过点P作PF⊥x轴于点F,则
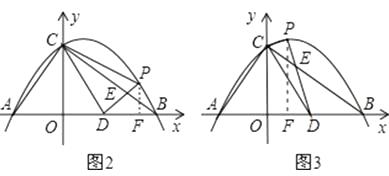
S△CDP=S梯形COFP﹣S△COD﹣S△DFP
= ![]() =m+n﹣2
=m+n﹣2
= ![]() =
= ![]()
∴当m= ![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为( ![]() ,
, ![]() ),
),
S△CDP的最大值是 ![]()
【解析】(1)利用相似三角形的性质对应边成比例可列出比例式,构建方程;求出A、B、C坐标代入解析式即可 ;(2)△BDE是等腰三角形可分为三类:BD=BE或DB=DE或EB=ED;(3)最值问题的基本解决办法是函数思想,用m的代数式表示面积,通过P向x轴作垂线,构造梯形,作差法表示三角形面积,构建函数,利用配方法求出最值.

 名校课堂系列答案
名校课堂系列答案









