Question

【题目】数学阅读：

古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式：若一个三角形的三边长分别为a、b、c，则这个三角形的面积为，其中.这个公式称为“海伦公式”．

数学应用：

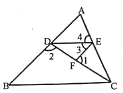
如图1，在△ABC中，已知AB=9，AC=8，BC=7.

（1）请运用海伦公式求△ABC的面积；

（2）设AB边上的高为，AC边上的高，求的值；

（3）如图2，AD、BE为△ABC的两条角平分线，它们的交点为I，求△ABI的面积．

Answer 1

【答案】（1） △ABC面积是；（2）；（3）S△ABC =

【解析】分析：（1）直接代入海伦公式计算.(2)利用海伦公式求出面积，再用一般求三角形面积公式求高.(2)角平分线的交点，到各个边的距离相等，所以可以用三个三角形的面积等于总面积，且高都相等，列方程可求出角分线到各边的距离.

详解：

（1） =12△ABC面积是 .

（2）等面积法求出，

（3）如图，过点I作IF⊥AB、IG⊥AC、IH⊥BC，垂足分别为点F、G、H，

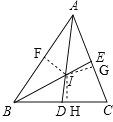
∵AD、BE分别为△ABC的角平分线，∴IF=IH=IG，

∵S△ABC=S△ABI+S△ACI+S△BCI， ∴（9IF+8IF+7IF）=，解得IF=

故S△ABC =ABFI=．