题目内容
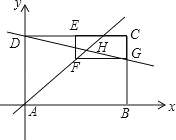
【题目】如图1,正方形ABCD的边长为8,⊙O经过点C和点D,且与AB相切于点E.
(1)求⊙O的半径;
(2)如图2,平移⊙O,使点O落在BD上,⊙O经过点D,BC与⊙O交于M,N,求MN2的值.

【答案】(1)5(2)160![]() ﹣206
﹣206
【解析】
试题分析:(1)如图1中,连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
(2)如图2中,作OP⊥BC于P,连接ON,则OD=ON=5,在Rt△OPN中,求出PN2即可解决问题.
试题解析:(1)连接EO,延长EO交CD于F,连接DO,设半径为x.

∵AB切○O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴x2=(8﹣x)2+42,
∴x=5,
∴⊙O的半径为5.
(2)如图2中,作OP⊥BC于P,连接ON,则OD=ON=5,

∵四边形ABCD是正方形,
∴BD=8![]() ,OB=BD﹣OD=8
,OB=BD﹣OD=8![]() ﹣5,OP=
﹣5,OP=![]() =8﹣
=8﹣![]() ,
,
∴PN2=ON2﹣OP2=52﹣(8﹣![]() )2=40
)2=40![]() ﹣51.5,
﹣51.5,
∵MN=2PN,
∴MN2=4PN2=4(40![]() ﹣51.5)=160
﹣51.5)=160![]() ﹣206.
﹣206.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目