题目内容
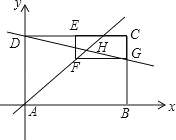
【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-![]() x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.
(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
【答案】(1)4(2)(![]() ,
,![]() )(3)直线BE过点H
)(3)直线BE过点H
【解析】
试题分析:(1)根据矩形性质和直线DG的与y轴的交点,确定出点C,B,D的坐标,即可;
(2)由两条直线的解析式联立即可求出点H的坐标;
(3)确定出直线BE的解析式,再判断点H是否在该直线上.
试题解析:(1)∵直线DG的函数表达式为y=﹣![]() x+4,
x+4,
∴D(0,4),
∵四边形ABCD是矩形,且C(6,m),
∴m=4,
∴C(6,4)
(2)∵直线AF:y=x与直线DG:y=﹣![]() x+4的交点为H,
x+4的交点为H,
∴ ,
,
∴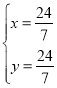 ,
,
∴H(![]() ,
,![]() )
)
(3)直线BE过点H,
理由:
∵直线DG解析式为y=﹣![]() x+4,直线BC解析式为x=6,
x+4,直线BC解析式为x=6,
∴G(6,3),
∴点F的纵坐标为3,
∵点F在直线AF上,
∴F点的横坐标为3,
∴F(3,3),
∴点E的横坐标为3,
∵直线DC解析式为y=4,
∴E(3,4),
∵B(6,0),
∴直线BE解析式为y=﹣![]() x+8,
x+8,
当x=![]() 时,y=﹣
时,y=﹣![]() ×
×![]() +8=
+8=![]() ,
,
∴直线BE过点H.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目