Ő‚ńŅńŕ»›
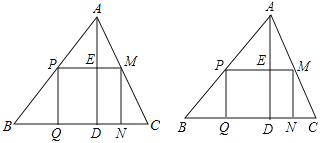
°ĺŐ‚ńŅ°Ņ»ÁÕľ£ļ”–“ĽŅť”ŗŃŌĶń–ő◊ī «»ŮĹ«»żĹ«–őABC£¨ĪŖBC=120mm£¨łŖAD=80mm£ģ
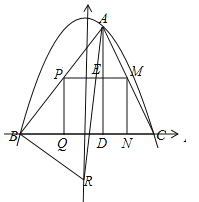
£®1£©»ÁĻŻį—ňŁľ”Ļ§≥…≥§∑Ĺ–őŃ„ľĢ£¨ Ļ≥§∑Ĺ–őĶń“ĽĪŖ‘ŕBC…Ō£¨∆š”ŗŃĹłŲ∂•Ķ„∑÷Īū‘ŕAB°ĘAC…Ō£¨…Ť≥§∑Ĺ–őŅŪxmm£¨√śĽżő™ymm2£¨ń«√īŅŪő™∂ŗ…Ŕ Ī£¨∆š√śĽż◊Óīů£ģ◊Óīů√śĽż «∂ŗ…Ŕ£Ņ
(2£©»Ű“‘BCĶń÷–Ķ„Oő™‘≠Ķ„Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨B£®-60£¨0£©£¨AD=BD£ģ
«ůĻżA°ĘB°ĘC»żĶ„ĶńŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
‘ŕīňŇ◊őÔŌŖ∂‘≥∆÷Š…Ō «∑Ůīś‘ŕ“ĽĶ„R£¨ Ļ“‘A°ĘB°ĘRő™∂•Ķ„Ķń»żĹ«–ő «÷ĪĹ«»żĹ«–ő£ģ»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥ŲRĶ„Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£© ĶĪx£Ĺ40 Ī£¨y◊Óīů÷Ķ£Ĺ2400 £Ľ£®2£©![]() £Ľ£®3£©ľŻĹ‚őŲ£ģ
£Ľ£®3£©ľŻĹ‚őŲ£ģ
°ĺĹ‚őŲ°Ņ∑÷őŲ£ļ£®1£©…ŤPQ=x£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√≥ŲQN=©Ā![]() x+120£¨łýĺ›ĺō–őĶń√śĽżĻę ĹľīŅ…Ķ√≥Ųy=©Ā
x+120£¨łýĺ›ĺō–őĶń√śĽżĻę ĹľīŅ…Ķ√≥Ųy=©Ā![]() x2+120x£¨Ňš∑ĹļůľīŅ…’“≥Ų√śĽżĶń◊Óīů÷Ķ£Ľ
x2+120x£¨Ňš∑ĹļůľīŅ…’“≥Ų√śĽżĶń◊Óīů÷Ķ£Ľ
£®2£©ĘŔ“ņ’’Ő‚“‚Ľ≠≥ŲÕľ–ő£¨”…ADĶń≥§∂»Ņ…Ķ√≥ŲĶ„AĶń◊ÝĪÍ£¨łýĺ›Ķ„A°ĘBĶń◊ÝĪÍ£¨ņŻ”√īż∂®ŌĶ ż∑®ľīŅ…«ů≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
Ęŕ…ŤĶ„RĶń◊ÝĪÍő™£®0£¨n£©£¨‘ÚAB=80![]() £¨AR=
£¨AR=![]() £¨BR=
£¨BR=![]() £¨∑÷°ŌABR=90°„°Ę°ŌARB=90°„ļÕ°ŌBAR=90°„»ż÷÷«ťŅŲŅľ¬«£¨ņŻ”√ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĻō”ŕnĶń“Ľ‘™“Ľīő£®ĽÚ“Ľ‘™∂Ģīő£©∑Ĺ≥Ő£¨Ĺ‚÷ģľīŅ…Ķ√≥ŲĹŠ¬Ř£ģ
£¨∑÷°ŌABR=90°„°Ę°ŌARB=90°„ļÕ°ŌBAR=90°„»ż÷÷«ťŅŲŅľ¬«£¨ņŻ”√ĻīĻ…∂®ņŪľīŅ…Ķ√≥ŲĻō”ŕnĶń“Ľ‘™“Ľīő£®ĽÚ“Ľ‘™∂Ģīő£©∑Ĺ≥Ő£¨Ĺ‚÷ģľīŅ…Ķ√≥ŲĹŠ¬Ř£ģ
ŌÍĹ‚£ļ£®1£©°ŖPQ°ÕBC£¨MN°ÕBC£¨AD°ÕBC£¨°ŗPQ°őAD£¨MN°őAD£¨°ŗ°ųBPQ°◊°ųBAD£¨°ųCAD°◊°ųCMN£¨°ŗBQ=![]() BD£¨CN=
BD£¨CN=![]() CD£ģ
CD£ģ
…ŤPQ=x£¨‘ÚQN=BC©ĀBQ©ĀCN=120©Ā![]() £®BD+CD£©=©Ā
£®BD+CD£©=©Ā![]() x+120£¨
x+120£¨
°ŗy=PQQN=x£®©Ā![]() x+120£©=©Ā
x+120£©=©Ā![]() x2+120x=©Ā
x2+120x=©Ā![]() £®x©Ā40£©2+2400£¨
£®x©Ā40£©2+2400£¨
°ŗĶĪx=40 Ī£¨y»°◊Óīů÷Ķ2400£¨°ŗŅŪő™40mm Ī£¨∆š√śĽż◊Óīů£ģ◊Óīů√śĽż «2400mm2£ģ
£®2£©ĘŔ“ņ’’Ő‚“‚Ľ≠≥ŲÕľ–ő£¨»ÁÕľňý ĺ£ģ
…ŤŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=ax2+c£¨ĹęB£®©Ā60£¨0£©°ĘA£®20£¨80£©īķ»Žy=ax2+c£¨![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ £¨°ŗĻżA°ĘB°ĘC»żĶ„ĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=©Ā
£¨°ŗĻżA°ĘB°ĘC»żĶ„ĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=©Ā![]() x2+90£ģ
x2+90£ģ
ĘŕľŔ…Ťīś‘ŕ£¨…ŤĶ„RĶń◊ÝĪÍő™£®0£¨n£©£¨‘ÚAB=80![]() £¨AR=
£¨AR=![]() £¨BR=
£¨BR=![]() £ģ
£ģ
∑÷»ż÷÷«ťŅŲŅľ¬«£ļ
ĘŔĶĪ°ŌABR=90°„ Ī£¨”–AR2=AB2+BR2£¨ľī400+£®80©Ān£©2=12800+3600+n2£¨Ĺ‚Ķ√£ļn=©Ā60£¨īň ĪĶ„RĶń◊ÝĪÍő™£®0£¨©Ā60£©£Ľ
ĘŕĶĪ°ŌARB=90°„ Ī£¨”–AB2=AR2+BR2£¨ľī12800=400+£®80©Ān£©2+3600+n2£¨’ŻņŪĶ√£ļn2©Ā80n©Ā1200=0£¨Ĺ‚Ķ√£ļn1=![]() £¨n2=
£¨n2=![]() £¨īň ĪĶ„RĶń◊ÝĪÍő™£®0£¨
£¨īň ĪĶ„RĶń◊ÝĪÍő™£®0£¨![]() £©ĽÚ£®0£¨
£©ĽÚ£®0£¨![]() £©£Ľ
£©£Ľ
ĘŘĶĪ°ŌBAR=90°„ Ī£¨”–BR2=AB2+AR2£¨ľī3600+n2=12800+400+£®80©Ān£©2£¨Ĺ‚Ķ√£ļn=100£¨īň ĪĶ„RĶń◊ÝĪÍő™£®0£¨100£©£ģ
◊Ř…Ōňý Ų£ļ‘ŕīňŇ◊őÔŌŖ∂‘≥∆÷Š…Ōīś‘ŕ“ĽĶ„R£¨ Ļ“‘A°ĘB°ĘRő™∂•Ķ„Ķń»żĹ«–ő «÷ĪĹ«»żĹ«–ő£¨Ķ„RĶń◊ÝĪÍő™£®0£¨©Ā60£©ĽÚ£®0£¨![]() £©ĽÚ£®0£¨
£©ĽÚ£®0£¨![]() £©ĽÚ£®0£¨100£©£ģ
£©ĽÚ£®0£¨100£©£ģ