题目内容
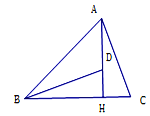
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
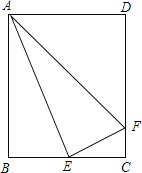
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
【答案】C
【解析】
试题分析:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵EF⊥AE,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
故(1)正确;
(2)∵△ABE∽△ECF,
∴![]() ,
,
∵E是BC的中点,
即BE=EC,
∴![]() ,
,
在Rt△ABE中,tan∠BAE=![]() ,
,
在Rt△AEF中,tan∠EAF=![]() ,
,
∴tan∠BAE=tan∠EAF,
∴∠BAE=∠EAF,
∴AE平分∠BAF;
故(2)正确;
(3)∵当k=1时,即![]() =1,
=1,
∴AB=AD,
∴四边形ABCD是正方形,
∴∠B=∠D=90°,AB=BC=CD=AD,
∵△ABE∽△ECF,
∴![]() ,
,
∴CF=![]() CD,
CD,
∴DF=![]() CD,
CD,
∴AB:AD=1,BE:DF=2:3,
∴△ABE与△ADF不相似;
故(3)错误.
故选C.

练习册系列答案
相关题目