题目内容
【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.

【答案】(1)见解析;(2)见解析;(3)∠ACF=60°
【解析】
(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;
(2)延长AE交CF于D,根据三角形的内角和得∠CDE=∠ABC=90°;
(3)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:
∵∠ABC=90°
∴∠ABE=∠CBF=90°
∴△ABE和△CBF是直角三角形
∵AB=BC,AE=CF
∴Rt△ABE≌Rt△CBF(HL)
(2)延长AE交CF于D,
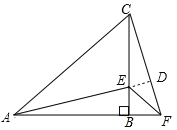
∵△ABE≌△CBF
∴∠BAE=∠BCF
∵∠AEB=∠CED
∴∠BAE+∠AEB=90°
∴∠DCE+∠CED=90°
∴∠CDE=90°
∴AE⊥CF.
(3)∵AB=CB,∠ABC=90°,∠CAE=30°,∠CAB=∠CAE+∠EAB,
∴∠BCA=∠BAC=45°,
∴∠EAB=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠FCB,
∴∠FCB=15°,
∴∠ACF=∠FCB+∠BCA=15°+45°=60°,
即∠ACF=60°.

【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。

