题目内容
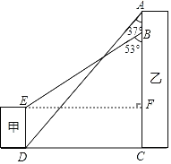
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为37°,走到乙楼B点处看甲楼楼顶E点处的俯角为53°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,精确到0.1m)
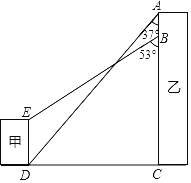
【答案】乙楼的高度AC的长为36.7米
【解析】
过点E作EF⊥AC于点F,根据题意,可得四边形DEFC是矩形,EF=DC,FC=ED=10,再根据锐角三角函数即可求出BF的长,进而可得乙楼的高度AC的长.
解:如图,过点E作EF⊥AC于点F,
根据题意,可得四边形DEFC是矩形,
∴EF=DC,FC=ED=10,
∴在Rt△ADC中,DC=ACtan37°≈0.75(AB+BF+FC)≈0.75(16+BF),
在Rt△BEF中,EF=AFtan53°≈1.33(6+BF),
∴0.75(16+BF)=1.33(6+BF),
解得BF≈20.7,
∴AC≈16+20.7≈36.7(m).
答:乙楼的高度AC的长为36.7米.

练习册系列答案
相关题目