题目内容
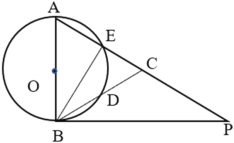
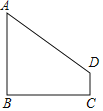
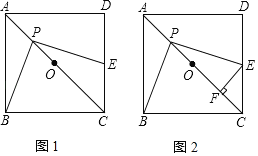
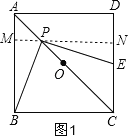
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与点A,O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.
(1)求证:PE=PB;
(2)如图2,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由;
(3)用等式表示线段PC,PA,CE之间的数量关系.
【答案】(1)见解析;(2)在P点运动的过程中,PF的长度不发生变化.PF的长为定值![]() ;(3)
;(3)![]() .理由见解析.
.理由见解析.
【解析】
(1)做辅助线,构建全等三角形,根据ASA证明![]() 即可求解.
即可求解.
(2)如图,连接OB,通过证明![]() ,得到PF=OB,则PF为定值是
,得到PF=OB,则PF为定值是![]() .
.
(3)根据△AMP和△PCN是等腰直角三角形,得![]() ,
,![]() ,整理可得结论.
,整理可得结论.
(1)证明:如图①,过点P作MN∥AD,交AB于点M,交CD于点N.
∵PB⊥PE,
∴∠BPE=90°,
∴∠MPB+∠EPN=90°.
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°.
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D=90,
∵∠MPB+∠MBP=90°,
∴∠EPN=∠MBP.
在Rt△PNC中,∠PCN=45°,
∴△PNC是等腰直角三角形,
∴PN=CN,
∴BM=CN=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE.
(2)解:在P点运动的过程中,PF的长度不发生变化.
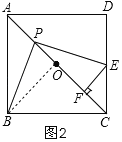
理由:如图2,连接OB.
∵点O是正方形ABCD对角线AC的中点,
∴OB⊥AC,
∴∠AOB=90°,
∴∠AOB=∠EFP=90°,
∴∠OBP+∠BPO=90°.
∴∠BPE=90°,
∴∠BPO+∠OPE=90°,
∴∠OBP=∠OPE.
由(1)得PB=PE,
∴△OBP≌△FPE(AAS),
∴PF=OB.
∵AB=2,△ABO是等腰直角三角形,∴![]() .
.
∴PF的长为定值![]() .
.
(3)解:![]() .
.
理由:如图1,∵∠BAC=45°,
∴△AMP是等腰直角三角形,
∴![]() .
.
由(1)知PM=NE,
∴![]() .
.
∵△PCN是等腰直角三角形,
∴![]() .
.

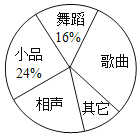
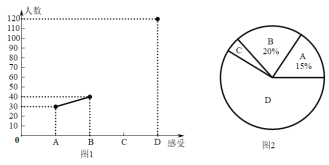
【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.