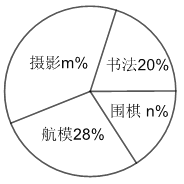
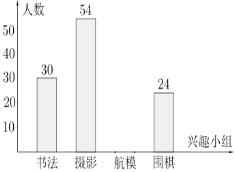
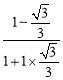题目内容
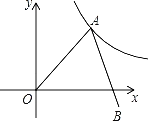
【题目】如图,反比例函数y=![]() (x>0)的图象上有一点A,连结OA,将线段AO绕点A逆时针旋转60°得到线段AB.若点A的横坐标为t,点B的纵坐标为s,则s关于t的函数解析式为_____.
(x>0)的图象上有一点A,连结OA,将线段AO绕点A逆时针旋转60°得到线段AB.若点A的横坐标为t,点B的纵坐标为s,则s关于t的函数解析式为_____.
【答案】s=![]() ﹣
﹣![]() t
t
【解析】
作AC⊥x轴于C,则OC与AC的长分别代表A点的横坐标与纵坐标,连接OB,则△AOB是等边三角形,以OC为边向下构造等边△OCD,连接BD,则可得△BOD≌△AOC,于是BD=AC,作DF⊥y轴于F,BE⊥DF于E,可得△OFD与△BDE均为含30°的直角三角形,于是OF与BE均可用t表示,B点的纵坐标也就可以用t表示了.
解:由题意知A(t,![]() ),则OC=t,AC=
),则OC=t,AC=![]() .
.
如图,作AC⊥x轴于C,以OC为边向下构造等边△OCD,作DF⊥y轴于F,BE⊥DF于E,连接OB、BD.
∴OC=OD=t,∠COD=60°,∠ACO=90°,∠OFD=∠DEB=90°,
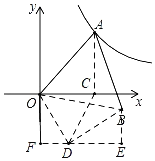
∵AO=AB,∠OAB=60°,
∴△AOB为等边三角形,
∴OB=OA,∠AOB=60°,
∴∠BOD=∠AOC,
∴△BOD≌△AOC(SAS),
∴∠BDO=∠ACO=90°,BD=AC=![]() ,
,
∴∠ODF+∠BDE=90°,
∵∠ODF+∠DOF=90°,
∴∠DOF=∠BDE,
∵∠DOF=90°﹣∠COD=30°,
∴DF=![]() OD=
OD=![]() t,OF=
t,OF=![]() OD=
OD=![]() t,BE=
t,BE=![]() BD=
BD=![]() ,
,
∴s=﹣(OF﹣BE)=![]() ﹣
﹣![]() t.
t.
故答案为:s=![]() ﹣
﹣![]() t.
t.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目