题目内容
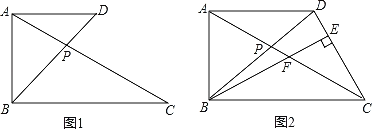
【题目】如图1,共直角边AB的两个直角三角形中,∠ABC=∠BAD=90°,AC交BD于P,且tan∠C=![]() .
.
(1)求证:AD=AB;
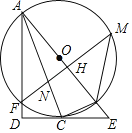
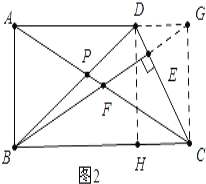
(2)如图2,BE⊥CD于E交AC于F.
①若F为AC的中点,求![]() 的值;
的值;
②当∠BDC=75°时,请直接写出![]() 的值.
的值.
【答案】(1)证明见解析;(2)①![]() ,②
,②![]()
【解析】
(1)根据AD∥BC得![]() =
=![]() ,又tan∠C=
,又tan∠C=![]() 故
故![]() ,故AD=AB.
,故AD=AB.
(2)①在图2中,过D作DH⊥BC于H,延长BE交AD延长线于G,易证ABHD为正方形,设其边长为a,DG=b,根据△ABC∽△DGC,得到a、b的关系即可解决问题.
②根据条件推出∠HDC=30°,设CH=m,则DC=2CH=2m,BH=DH=![]() mc,从而表示出EC和DE,即可求出结论.
mc,从而表示出EC和DE,即可求出结论.
解:(1)∵∠DAB+∠ABC=180°,
∴AD∥BC,
∴![]() =
=![]() ,
,
∵tan∠C=![]() =
=![]()
∴![]() ,
,
∴AD=AB.
(2)①在图2中,过D作DH⊥BC于H,延长BE交AD延长线于G,连接CG,易证ABHD为正方形,设其边长为a,DG=b,
∵AG∥BC,
∴![]() ,
,
∵AF=FC,
∴AG=BC,
∴四边形ABCG是平行四边形,
∵∠ABC=90°
∴四边形ABCG是矩形,
∴FB=FC,∠BCG=∠AGC=90°,
∴∠FBC=∠FCB,
∵∠FBC+∠BCE=90°,∠BCE+∠ECG=90°,
∴∠ECG=∠FBC,
∴∠DCG=∠ACB,
∵∠ABC=∠DGC=90°
∴△ABC∽△DGC,
∴![]() ,
,
∴![]() ,
,
∴a2﹣ab﹣b2=0,
∴a=![]() (或a=
(或a=![]() 舍弃),
舍弃),
∵DG∥BC,
∴![]() =
=![]() =
=![]() =
=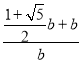 =
=![]() ,
,
②由1可知四边形ABHD是正方形,
∴∠BDH=45°,BH=DH
∵∠BDC=75°,
∴∠HDC=30°,∠DCH=60°
设CH=m,则DC=2CH=2m,BH=DH=![]() m
m
∴EC=BC·cos∠DCH=![]() (m+
(m+![]() m),DE=DC﹣CE=2m﹣
m),DE=DC﹣CE=2m﹣![]() (m+
(m+![]() m),
m),
∴![]() =
=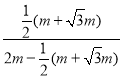 =
=![]() .
.

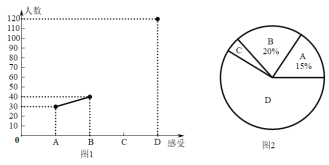
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

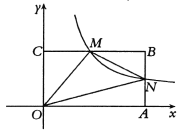
(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?