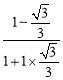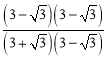题目内容
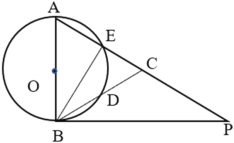
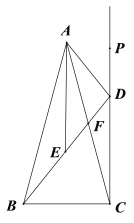
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
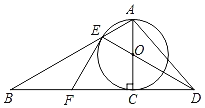
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
【答案】(1)见解析;(2)AD=![]() .
.
【解析】
(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
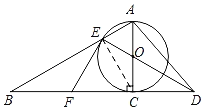
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=![]() .
.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=![]() .
.
∴AD=![]() =
=![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目