题目内容
【题目】如图，在平面直角坐标系中，△ABO为底角是30°的等腰三角形，OA＝AB＝4，O为坐标原点，点B在x轴上，点P在直线AB上运动，当线段OP最短时，点P的坐标为（ ）
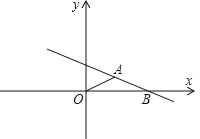
A. （1，1） B. （
，3） C. （3，） D. （2，2）
【答案】B
【解析】
过点O作OP⊥AB与P，过A作AC⊥OB与C，则此时OP的长度最短，在△OAB中求出OB的长度，然后利用含30°角的直角三角形的性质可得出OP的长度．
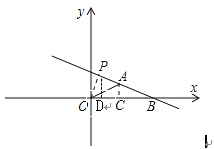
解：过点O作OP⊥AB于P，过A作AC⊥OB于C，
∵∠AOB=∠ABO=30°，∠POB=60°
∴OC=
OA=2
，OB=OC+CB=4，
∴OP=
OB=2，
过P点作OD⊥x轴于D，则∠PDO=90°
∵∠POB=60°∴OD=, PD=3
∴P（，3）．
故选：B．
练习册系列答案
相关题目
