题目内容
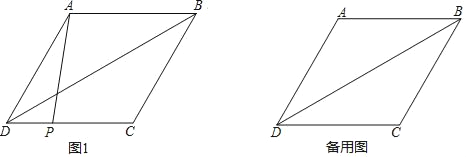
【题目】在菱形ABCD中,∠ADC=60°,BD是一条对角线,点P在边CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,在BD上取一点H,使HQ=HD,连接HQ,AH,PH.
(1)依题意补全图1;
(2)判断AH与PH的数量关系及∠AHP的度数,并加以证明;
(3)若∠AHQ=141°,菱形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
【答案】(1)见解析;(2)AH=PH,∠AHP=120°,理由见解析;(3)见解析
【解析】
(1)根据题意可补全图形;
(2)由平移的性质可得PQ=CD,由菱形的性质可得AD=DC,∠ADB=∠BDQ=30![]() ,可得AD=PQ,∠HQD=∠HDQ=30
,可得AD=PQ,∠HQD=∠HDQ=30![]() ,可证△ADH≌△PQH,可得AH=PH,∠AHD=∠PHE,即可求出∠AHP=120
,可证△ADH≌△PQH,可得AH=PH,∠AHD=∠PHE,即可求出∠AHP=120![]() ,
,
(3)根据三角形的内角和定理和等腰三角形的性质可求∠DAP=21![]() ,通过解△DAP,可求DP的长度.
,通过解△DAP,可求DP的长度.
解:(1)补全图形,如图所示
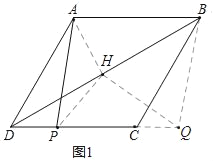
(2)AH=PH,∠AHP=120°.
理由如下:如图,由平移可知,PQ=DC.
∵四边形ABCD是菱形,∠ADC=60°,
∴AD=DC,∠ADB=∠BDQ=30°,
∴AD=PQ,
∵HQ=HD,
∴∠HQD=∠HDQ=30°,
∴∠ADB=∠DQH,∠DHQ=120°.
∵HQ=DH,∠ADB=∠DQH,AD=PQ,
∴△ADH≌△PQH(SAS),
∴AH=PH,∠AHD=∠PHQ,
∴∠AHD+∠DHP=∠PHQ+∠DHP,
∴∠AHP=∠DHQ,
∵∠DHQ=120°,
∴∠AHP=120°.
(3)求解思路如下:
由∠AHQ=141°,∠BHQ=60°解得∠AHB=81°,
a.在△ABH中,由∠AHB=81°,∠ABD=30°,解得∠BAH=69°,
b.在△AHP中,由∠AHP=120°,AH=PH,解得∠PAH=30°,
c.在△ADB中,由∠ADB=∠ABD=30°,解得∠BAD=120°,
由a、b、c可得∠DAP=21°,
在△DAP中,由∠ADP=60°,∠DAP=21°,AD=1,可解△DAP,
从而求得DP长.