题目内容
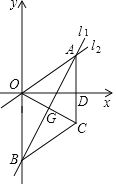
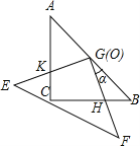
【题目】把两个全等的等腰直角三角板ABC和EFG叠放在一起,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分,已知AC=4.在旋转过程中,下列结论:①BH=CK;②四边形CHGK的面积等于4;③GK长度的最大值为2![]() ;④线段KH的长度最小值为2
;④线段KH的长度最小值为2![]() .其中正确的有( )个
.其中正确的有( )个
A.1B.2C.3D.4
【答案】D
【解析】
由等腰直角三角形的性质可判断③,”ASA“可证△BGH≌△CGK,可得CK=BH,S△CKG=S△BHG,可判断①②,由勾股定理和二次函数性质可判断④.
解:连接CG,
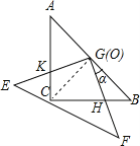
∵AC=BC=4,∠ACB=90°,G是AB中点,
∴∠ACG=∠B=45°,AB=4![]() ,CG=BG=2
,CG=BG=2![]() ,CG⊥AB,
,CG⊥AB,
∴当点K与点C重合时,GK有最大值为2![]() ,
,
故③正确,
∵∠KGH=∠CGB=90°,
∴∠KGC=∠BGH,且CG=BG,∠B=∠GCA,
∴△BGH≌△CGK(ASA),
∴CK=BH,S△CKG=S△BHG,
∴S四边形CKGH=S△BGC=![]() S△BCA=4,
S△BCA=4,
故①②正确,
∵BH=CK
∴CH=4-CK
∵KH2=(4-CK)2+CK2=2(CK-2)2+8
∴当CK=2时,KH有最小值2![]()
故④正确
故选:D.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?