Question

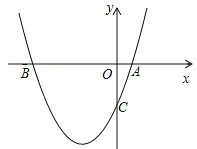
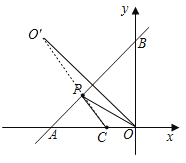
【题目】如图，直线y＝x+b与x轴交于点A，与y轴于点B，点C(﹣2，0)在线段OA上，且OC＝OA．

（1）求b的值；

（2）点P是直线y＝x+b上一动点，连接PC，PO，求PC+PO的最小值．

Answer 1

【答案】（1）6；（2）2

【解析】

（1）根据题意求得OA，得出A的坐标，把A（﹣6，0）代入y＝x+b，即可求得b的值；

（2）过O作直线AB的对称点O′，连接O′C交AB于点P，此时PC+PO的值最小，最小值为O′C的长，求得O′的坐标，然后根据勾股定理即可求得．

解：（1）∵点C（﹣2，0）在线段OA上，且OC＝OA，

∴OA＝3OC＝3×2＝6，

∴A（﹣6，0），

∵直线y＝x+b与x轴交于点A，

∴﹣6+b＝0，

∴b＝6；

（2）过O作直线AB的对称点O′，连接O′C交AB于点P，此时PC+PO的值最小，最小值为O′C的长，

∵直线为y＝x+6，

∴B（0，6），

∴OA＝OB＝6，

∴△AOB是等腰直角三角形，

∴∠BAO＝45°，

∵OO′和AB互相垂直平分，

∴四边形AOBO′是正方形，

∴O′（﹣6，6），

∴，

故PC+PO的最小值为2．