题目内容
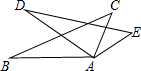
如图，正方形ABCD的边长为1，EF分别在BC、CD上，∠EAF=45°，若△CEF的面积为
，则△EAF的面积为______．
| 1 |
| 4 |
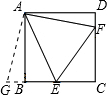
将△ADF绕点A逆时针旋转90°，得到△ABG，如图，
∴∠ADF=∠ABG=90°，DF=BG，AF=AG，∠FAG=90°，
∴点G在CB的延长线上，
而∠EAF=45°，
∴∠GAE=45°，
∴△FAE≌△GAE，
∴S正方形ABCD=2S△AEF+S△EFC，
∴2S△AEF=1×1-
=
，
∴S△AEF=
．
故答案为
．
∴∠ADF=∠ABG=90°，DF=BG，AF=AG，∠FAG=90°，
∴点G在CB的延长线上，
而∠EAF=45°，
∴∠GAE=45°，
∴△FAE≌△GAE，
∴S正方形ABCD=2S△AEF+S△EFC，
∴2S△AEF=1×1-
| 1 |
| 4 |
| 3 |
| 4 |
∴S△AEF=
| 3 |
| 8 |
故答案为
| 3 |
| 8 |
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
