题目内容
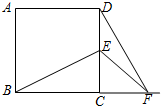
把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=12，CD=14，把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长度为______．
由题意易知：∠CAB=45°，∠ACD=30°．
若旋转角度为15°，则∠ACO=30°+15°=45°．
∴∠AOC=180°-∠ACO-∠CAO=90°．
在等腰Rt△ABC中，AB=12，则AC=BC=6
．
同理可求得：AO=OC=6．
在Rt△AOD1中，OA=6，OD1=CD1-OC=8，
由勾股定理得：AD1=10．
故答案为：10．
若旋转角度为15°，则∠ACO=30°+15°=45°．
∴∠AOC=180°-∠ACO-∠CAO=90°．
在等腰Rt△ABC中，AB=12，则AC=BC=6
| 2 |
同理可求得：AO=OC=6．
在Rt△AOD1中，OA=6，OD1=CD1-OC=8，
由勾股定理得：AD1=10．
故答案为：10．
练习册系列答案
智能训练练测考系列答案
相关题目
