题目内容
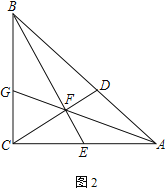
【题目】如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，弧AC，弧BC的中点分别是M，N，P，Q. 若MP+NQ=14，AC+BC=18，则AB的长是【 】
A. 
B. 
C. 13 D. 16
【答案】C
【解析】连接OP，OQ，根据DE，FC，
，
的中点分别是M，N，P，Q得到OP⊥AC，OQ⊥BC，从而得到H、I是AC、BD的中点，利用中位线定理得到OH+OI=
（AC+BC）=9和PH+QI，从而利用AB=OP+OQ=OH+OI+PH+QI求解．
解：连接OP，OQ，
∵DE，FC，
，
的中点分别是M，N，P，Q，
∴OP⊥AC，OQ⊥BC，
∴H、I是AC、BD的中点，
∴OH+OI=
（AC+BC）=9，
∵MH+NI=AC+BC=18，MP+NQ=14，
∴PH+QI=18﹣14=4，
∴AB=OP+OQ=OH+OI+PH+QI=9+4=13，
故选C．
“点睛”本题考查了中位线定理，解题的关键是正确的作出辅助线，题目中还考查了垂径定理的知识，难度不大．
【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛，该运动队预先对这两名选手进行了8次测试，测得的成绩如表：
次数 | 选手甲的成绩（环） | 选手乙的成绩（环） |
1 | 9.6 | 9.5 |
2 | 9.7 | 9.9 |
3 | 10.5 | 10.3 |
4 | 10.0 | 9.7 |
5 | 9.7 | 10.5 |
6 | 9.9 | 10.3 |
7 | 10.0 | 10.0 |
8 | 10.6 | 9.8 |
根据统计的测试成绩，请你运用所学过的统计知识作出判断，派哪一位选手参加比赛更好？为什么？
【题目】大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足：当1≤x＜25时，q＝x＋60；当25≤x≤50时，q＝40＋
.
（1）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系；
（2）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式；
（3）这50天中，该超市第几天获得利润最大？最大利润为多少？
