题目内容
【题目】△ABC中，∠ACB＝90°，点E为AC的中点，CD⊥BE交AB于D点，交BE于点F
(1) 如图1，若AC＝2BC，求证：AD＝2BD
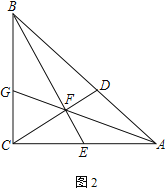
(2) 如图2，若∠ACD＝30°，连AF并延长交BC于G点，求
的值
(3) 在(1)的条件下，若AC＝4，以AB为边作等腰直角三角形ABM（点M与点C在AB异侧），直接写出CM的长
【答案】(1) 证明见解析(2) 
(3) 
、
、
【解析】(1) ∵E为AC的中点
∴CE＝AE
又AC＝2BC
∴BC＝CE
∵CF⊥BE
∴CF平分∠BCE
过点B作BF交CD的延长线于F
∴△BCF为等腰直角三角形
∴BF＝BC＝
AC
∵△BDF∽△ADC
∴
即AD＝2BD
(2) ∵∠CFE＝90°，∠ECF＝30°
∴AE＝CE＝2，EF＝1，CF＝
∵∠CBF＝30°
∴BF＝CF＝3
过点B作BH⊥BC交AG的延长线于H
∴
，BH＝6
∴
(3) 八年级的题目，一类是三垂直，一类是对角互补
、、
练习册系列答案
相关题目
