Question

【题目】已知抛物线y=ax2+bx+c（a＞0）与x轴的两个交点分别为A（﹣1，0）、B（3，0），与y 轴的交点为点D，顶点为C，

（1）写出该抛物线的对称轴方程；

（2）当点C变化，使60°≤∠ACB≤90°时，求出a的取值范围；

（3）作直线CD交x轴于点E，问：在y轴上是否存在点F，使得△CEF是一个等腰直角三角形？若存在，请求出a的值；若不存在，请说明理由．

Answer 1

【答案】（1）对称轴x=1　（2）当点C变化，使60°≤∠ACB≤90°时， ≤a≤； （3） a=或a=或a=．

【解析】（1）根据抛物线y=ax2+bx+c（a＞0）与x轴的两个交点分别为A（﹣1，0）、B（3，0），即可求出抛物线的对称轴；

（2）分别求出当∠ACB=60°和∠ACB=90°时a的值，进而求出使60°≤∠ACB≤90°时，求出a的取值范围；

（3）分别写出C点和D点的坐标以及E点的坐标，再进行分类讨论证明△EHF≌△EKC，列出a的方程，解出a的值．

解：（1）∵抛物线y=ax2+bx+c（a＞0）与x轴的两个交点分别为A（﹣1，0）、B（3，0），

∴抛物线的对称轴x==1；

（2）当∠ACB=60°时，△ABC是等边三角形，即点C坐标为（1，﹣2），

设y=a（x+1）（x﹣3），把C点坐标（1，﹣2）代入，

解得a=；

当∠ACB=90°时，△ABC是等腰直角三角形，即点C坐标为（1，﹣2），

设y=a（x+1）（x﹣3），把C点坐标（1，﹣2）代入，

解得a=，

即当点C变化，使60°≤∠ACB≤90°时， ≤a≤；

（3）由于C（1，﹣4a），D（0，﹣3a），

设直线CD的解析式为y=kx+b，

即，

解得k=﹣a，b=﹣3a，

直线CD的解析式为y=﹣a（x+3），

故求出E点坐标为（﹣3，0）；

分两类情况进行讨论；

如图1，

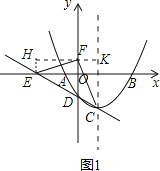
△EHF≌△FKC，

即HF=CK=3，

4a+1=3，

解得a=；

②如图2，

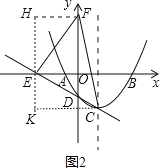
△EHF≌△FKC，

即EK=HF=3；

即4a=3，解得a=；

同理，当点F位于y轴负半轴上，a=．

综上可知在y轴上存在点F，使得△CEF是一个等腰直角三角形，且a=或a=或a=．

“点睛”本题主要考查二次函数的综合题的知识点，解答本题的关键是能够利用数形结合进行解题，此题的难度较大，特别是第三问需要进行分类讨论解决问题．