Question

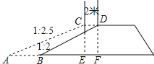
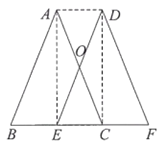
【题目】如图，在△ABC中，AB＝AC．将△ABC沿着BC方向平移得到△DEF，其中点E在边BC上，DE与AC相交于点O．

（1）求证：△OEC为等腰三角形；

（2）连接AE、DC、AD，当点E在什么位置时，四边形AECD为矩形，并说明理由．

Answer 1

【答案】（1）见解析；（2）当为中点时，四边形为矩形. 见解析.

【解析】

（1）根据等腰三角形的性质得出∠B＝∠ACB，根据平移得出AB∥DE，求出∠B＝∠DEC，再求出∠ACB＝∠DEC即可；

（2）求出四边形AECD是平行四边形，再由，求出四边形AECD是矩形即可．

（1）∵，∴.

∴平移得到，∴.

∴，∴.

即为等腰三角形.

（2）当为中点时，四边形为矩形.

∵，且为中点.

∴.

∵平移得到，

∴.

∴.

又∵，∴四边形为矩形.