��Ŀ����
����Ŀ��ijͨѶ��Ӫ�̵��ֻ����������ʷѱ��Ƴ��������Żݷ�����
����A:�������Ʒѣ�0.1Ԫ/M��
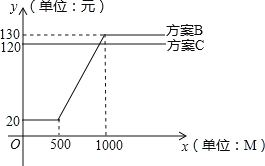
����B:20Ԫ�����ײͰ��£�����500M�������������500M��������������Ʒѣ���ͼ������õ�1000Mʱ������1000M�����������շѣ�
����C:120Ԫ���£�������ʹ��.
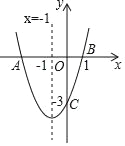
��x��ʾÿ����������(��λ��M),y��ʾÿ�µ���������(��λ��Ԫ)������B�ͷ���C��Ӧ��y����x�ĺ���ͼ����ͼ��ʾ�������������⣺
(1)д������A�ĺ�������ʽ������ͼ�л�����ͼ��
(2)ֱ��д������B�ĺ�������ʽ��
(3)����������ÿ��ʹ�������ֱ���300��600M��800��1200M֮�䣬����ֱ�������Ҷ��˾��ú�����ѡ��.
���𰸡�������
����������������1�����������Ʒѵ��ۼ��ɽ����
��2�����ݷ���B������ͼ����500��20������1000��130����������м��ֱ�ߵĽ���ʽ����д���ֶκ�������ʽ��
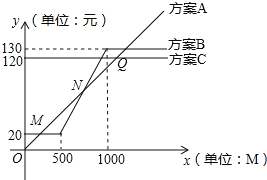
��3������ͼ���ݹؼ��㣬���ú���ͼ�������⣮
��⣺��1������A�ĺ�������ʽΪy=0.1x��ͼ����ͼ��ʾ��
��2����ͼ��֪����B������ͼ����500��20������1000��130����
��������м��ֱ�ߵĽ���ʽΪy=0.22x-90��
���B�Ľ���ʽΪ
y=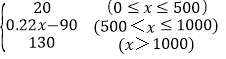 ��
��
��3����ͼ�跽��A�ĺ���ͼ���뷽��B�ĺ���ͼ���ڵ�M��N���뷽��C����ͼ��Ľ��ڵ�Q����M��200��20����N��750��75����Q��1200��120����
��ˣ�����������200M���µ�ѡ�÷���A��
����������200M��750M֮���ѡ�÷���B��
����������750M��1200M֮���ѡ�÷���A��
����������1200����M��ѡ�÷���C��
����������200M��750M��ѡ�÷���A��B����һ����
����������1200M��ѡ�÷���A��C����һ����

����Ŀ���ס�������ѧ���μ���ѧ���ʲ��ԣ��������ÿ����Գɼ����ðٷ��ƣ��ɼ������
ѧ�� | ������� | �ռ���ͼ�� | ͳ������� | �ۺ���ʵ�� | ƽ���ɼ� | ���� |
�� | 87 | 93 | 91 | 85 | 89 | ______ |
�� | 89 | 96 | 91 | 80 | ______ | ______ |
��1���������п�ȱ�����ݲ������������ݱ�����Ϣ�ж��ĸ�ѧ����ѧ�ۺ����ʲ��Գɼ����ȶ�����˵������.
��2��������������ռ���ͼ�Ρ�ͳ������ʡ��ۺ���ʵ���ijɼ���![]() �������ĸ�ѧ����ѧ�ۺ����ʲ��Գɼ����ã���˵������.
�������ĸ�ѧ����ѧ�ۺ����ʲ��Գɼ����ã���˵������.