Question

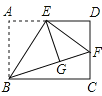
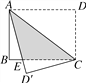
【题目】如图，长方形纸片ABCD沿对角线AC折叠，设点D落在D′处，BC交AD′于点E，AB＝6cm，BC＝8cm，求阴影部分的面积．

Answer 1

【答案】cm2.

【解析】

【试题分析】

因为四边形ABCD是长方形，根据矩形的性质得：∠B＝∠D＝90°，AB＝CD.由折叠的性质可知∠DAC＝∠EAC，因为AD//BC，根据平行线的性质，得∠DAC＝∠ECA，根据等量代换得，∠EAC＝∠ECA，根据等角对等边，得AE＝CE.设AE＝xcm，在Rt△ABE中，利用勾股定理得，AB2＋BE2＝AE2，即62＋(8－x)2＝x2，解得x＝，∴CE＝AE＝cm.∴S阴影＝·CE·AB＝××6＝ (cm2)．

【试题解析】

∵四边形ABCD是长方形，∴∠B＝∠D＝90°，AB＝CD.

由折叠的性质可知可知∠DAC＝∠EAC，∵AD//BC，

∴∠DAC＝∠ECA，∴∠EAC＝∠ECA，∴AE＝CE.

设AE＝xcm，在Rt△ABE中，AB2＋BE2＝AE2，即62＋(8－x)2＝x2，∴x＝，∴CE＝AE＝cm.∴S阴影＝·CE·AB＝××6＝ (cm2)．故答案为cm2.