题目内容
【题目】课外兴趣小组活动时,老师提出了如下问题: 如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,再连接BE,(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
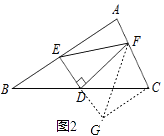
(1)解决问题:受到(1)的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF. ①求证:BE+CF>EF;
②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明
(2)问题拓展:如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明. 
【答案】
(1)解:①如图2,延长ED到点G,使DG=ED,连结GF,GC,
∵ED⊥DF,
∴EF=GF,
∵D是BC的中点,
∴BD=CD,
在△BDE和△CDG中,
 ,
,
∴△DBE≌△DCG(SAS),
∴BE=CG,
∵CG+CF>GF,
∴BE+CF>EF;
②线段BE、CF、EF之间的等量关系为:BE2+CF2=EF2.
证明:如图2,
∵∠A=90°,
∴∠B+∠ACB=90°,
由①可得,△DBE≌△DCG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,即∠GCF=90°,
∴Rt△CFG中,CF2+GC2=GF2,
∴BE2+CF2=EF2;
(2)解:线段BE、CF、EF之间的数量关系为:EF=BE+CF,
理由:如图3,延长AC到G,使CG=BE,

∵∠B+∠ACD=180°,∠ACD+∠DCG=180°,
∴∠B=∠DCG,
在△DBE和△DCG中,
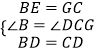 ,
,
∴△DBE≌△DCG(SAS),
∴DE=DG,∠BDE=∠CDG,
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°,
∴∠CDG+∠CDF=60°,
∴∠EDF=∠GDF,
在△EDF和△GDF中,
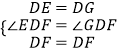 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵GF=CG+CF,
∴GF=BE+CF,
∴EF=BE+CF.
【解析】(1)①延长ED到点G使DG=ED,连结GF,GC,就有EF=GF,连结FG、CG,可证△BED≌△CDG,则CG=BE,由三角形的三边关系就可以得出结论;②由∠A=90°就可以得出∠A+∠ACB=90°,就可以得出∠FCG=90°,由勾股定理就可以得出结论;(2)延长AC到G使CG=BE,连结DG可以得出△DBE≌△DCG就有DE=DG,∠BDE=∠CDG,由∠BDC=120°,∠EDF=60°,可以得出∠BDE+∠CDF=60°,进而得出∠FDG=60°,就有∠EDF=∠GDF,得出△EDF≌△GDF,得出结论.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分 数 段 | 频数 | 频率 |
60≤x<70 | 9 | a |
70≤x<80 | 36 | 0.4 |
80≤x<90 | 27 | b |
90≤x≤100 | c | 0.2 |

请根据上述统计图表,解答下列问题:
(1)在表中,a= , b= , c=;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?





