��Ŀ����
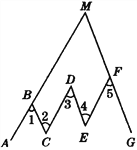
����Ŀ������У�ٰ�Ŀ����У���һ����С��������.��Ʒ�Ͻ�ʱ��Ϊ3��1����30�գ���ί���ͬѧ�ǽ�������Ʒ��ʱ��˳��ÿ5�����һ�飬��ÿһ��ļ�������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ.��֪�����Ҹ����εĸ߶ȱ�Ϊ2:3:4:6:4:1. ������ļ�����12��. ����ش�
(1)���λ����________����Ʒ������������Ʒ��������λ����________��.
(2)�����ȣ�������͵�����ֱ���10����2����Ʒ����ô����Ϊ���������ĸ�����ʽϸߣ�Ϊʲô��
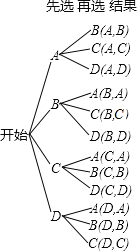
С�������Ƚ�������ί�������4�����������ƷA��B��C��D��ѡ����������ȫУչʾ��������״ͼ���б�������պ�չʾB��D�ĸ���.
���𰸡���1��60��10.5����2��������Ļ��ʽϸߣ����ɼ���������3��![]() .
.
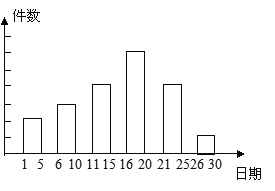
�������������������1������һ��Ϊx����4x=12���ɵ�x=3��һ����20�ݣ����Թ�60����ÿ�ݵļ���Ϊ6��9��12��18��12��3��������λ��Ϊ![]() ��
��
��2������������ô�����Ļ��ʣ���������ĸ�����ʽϸߣ�
��3��������Ҫ������ɣ����Բ�����״ͼ�����߲����б������Ƚϼ�����ʱҪע���ǷŻ�ʵ�黹�Dz��Ż�ʵ�飬�������ڲ��Ż�ʵ�飮
�����������1��60��10.5��
��2���⣺����������Ʒ![]() ��������
��������
����������Ʒ![]() ��������
��������
��������Ļ���Ϊ![]() ��������Ļ���Ϊ
��������Ļ���Ϊ![]() ��
��
��![]() ��
��![]() ��
��
��������Ļ��ʽϸߣ�
��3������״ͼ���£�
�������
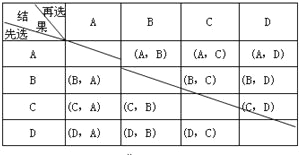
��ͼ������֪�����еȿ��ܵĽ����12�֣����иպ��ǣ�B��D������2�֣�
���Ըպ�չʾB��D�ĸ���Ϊ![]() ��
��
����: 1.�б�������״ͼ����2.Ƶ�����ʣ��ֲ�ֱ��ͼ��3.��λ����4.���ʹ�ʽ