题目内容
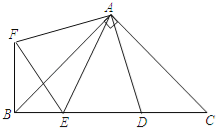
【题目】如图,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M.试探索∠AMG与∠3的关系,并说明理由.
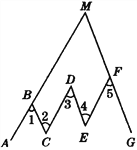
【答案】∠AMG=∠3.
【解析】试题分析:先根据内错角相等,两直线平行,可得: AB∥CD,根据内错角相等两直线平行,可得CD∥EF,根据平行于同一条直线的两直线平行可得: AB∥EF,再根据两直线平行,同位角相等,可得: ∠AMG=∠5,等量代换即可求证.
试题解析:∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
∵∠3=∠4,
∴CD∥EF(内错角相等,两直线平行),
∴AB∥EF(平行于同一条直线的两直线平行),
∴∠AMG=∠5(两直线平行,同位角相等),
又∠5=∠3,
∴∠AMG=∠3.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目