题目内容
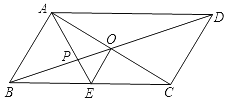
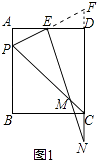
【题目】如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当 ![]() =时,E恰好是AD的中点;
=时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求 E N E M 的值. 
【答案】
(1)证明:延长PE交CD的延长线于F,如图1所示:
∵四边形ABCD是矩形,
∴AB∥CD,∠A=∠ADC=∠EDF═90°,AB=CD,AD=BC,
∴∠APE+∠AEP=90°,
∴∠F=∠APE,
∵EM⊥EN,
∴∠PEN=∠FEN=90°,
∴∠CPE+∠PME=90°,∠F+∠N=90°,
∵PE平分∠APC,
∴∠APE=∠MPE,
又∵∠PME=∠CMN,
∴∠CMN=∠N,
∴CM=CN
(2)["![]() ,解:分两种情况:①若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;②若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=
,解:分两种情况:①若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;②若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB= ![]() a,AP=(4﹣
a,AP=(4﹣ ![]() )a,AE=(4
)a,AE=(4 ![]() ﹣3)a,设PE与CD交于点F,如图3所示:
﹣3)a,设PE与CD交于点F,如图3所示:![]() ∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴
∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴ ![]() ,∵AB∥CD,∴
,∵AB∥CD,∴ ![]() ,∴
,∴ ![]() =
= ![]() =
= ![]() 【解析】(2)解:①若E是AD的中点,则M、N、C三点重合,
【解析】(2)解:①若E是AD的中点,则M、N、C三点重合,
∵E为AD的中点,
∴AE=DE,
在△APE和△DFE中, 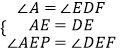 ,
,
∴△APE≌△DFE(ASA),
∴AP=DF,PE=FE,
∵EM⊥EN,
∴PC=FC,
∵FC=CD+DF,
∴AP+CD=PC,
设AD=3a,AB=4a,
过P作PF⊥CD于F,如图2所示:

设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,
由勾股定理得:(4﹣x)2+32=(4+x)2,
解得:x= ![]() a,4﹣x=
a,4﹣x= ![]() a,
a,
∴ ![]() ;
;
【考点精析】通过灵活运用角的平分线判定和对顶角和邻补角,掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个即可以解答此题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?