��Ŀ����
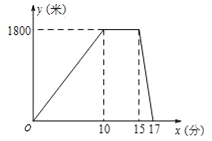
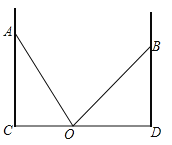
����Ŀ����ͼ1��������![]() �У�
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() �������
�������![]() ��·���ƶ�����
��·���ƶ�����![]() ʱֹͣ������ʱ��
ʱֹͣ������ʱ��![]() ��λ/�������˶���ͬʱ��
��λ/�������˶���ͬʱ��![]() ��
��![]() ������
������![]() ��·�������˶����ƶ�����
��·�������˶����ƶ�����![]() ʱֹͣ������ʱ��
ʱֹͣ������ʱ��![]() ��λ/���˶�,�����������
��λ/���˶�,�����������![]() �˶��ٶȱ�Ϊ
�˶��ٶȱ�Ϊ![]() ��λ/���˶�����
��λ/���˶�����![]() �˶��ٶȱ�Ϊ
�˶��ٶȱ�Ϊ![]() ��λ/���˶���ͼ2������
��λ/���˶���ͼ2������![]() ��
��![]() ���˶���������
���˶���������![]() ��ɨ����ͼ�ε����
��ɨ����ͼ�ε����![]() ��ʱ��
��ʱ��![]() �ĺ���ͼ��ͼ3������
�ĺ���ͼ��ͼ3������![]() ��
��![]() ���˶���������
���˶���������![]() ��ɨ����ͼ�ε����
��ɨ����ͼ�ε����![]() ��ʱ��
��ʱ��![]() ��ͼ��ͼ��
��ͼ��ͼ��
��1��������![]() �ı߳���______.
�ı߳���______.
��2����![]() ��
��![]() ������
������![]() ��������������ͼ�����
��������������ͼ�����![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
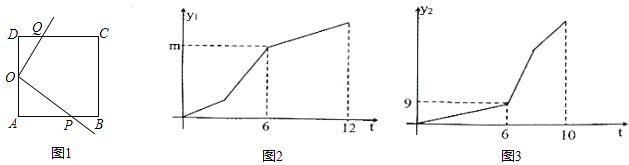
���𰸡���1��6����2�������.
��������
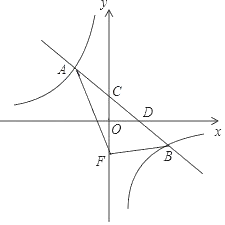
��1����ͼ3�п��Կ�������OQǰ��6��ɨ�������Ϊ9������Եõ�![]() ��
��![]() ADAD=9���Ӷ��ⷽ�̣���������εı߳�.
ADAD=9���Ӷ��ⷽ�̣���������εı߳�.
��2����ϸ�۲캯��ͼ���֪��P��Q���ڵ�C�����������ɣ�1���еõ��������α߳�����ã�����ǰ��P,Q���ٶȣ��ٻ���ͼ���г�ʽ����⼴��.
��:(1)��ͼ3��֪��OCD�����=9.
��O��AD���е㣬
��OD=![]() AD.
AD.
���ı���ABCD�������Σ�
��AD=CD����ODC=90�㣬
��![]() AD
AD![]() AD=9
AD=9
���:AD=6.
�ʴ�Ϊ6.
��2���۲�ͼ2��ͼ3��֪P��Q�������ڵ�C��������������ǰP��Q���ٶȷֱ�Ϊ2��1.������P,Q���˶��ٶȷֱ�Ϊ1��3.
�ٵ�6![]() t
t![]() ʱ����ͼ1��S=�����ε����-��POD�����-����OABQ�����.
ʱ����ͼ1��S=�����ε����-��POD�����-����OABQ�����. 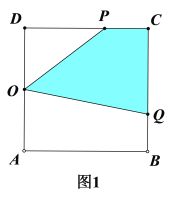
��PC=t-6,CQ=3(t-6)=3t-18.
��PD=12-t,BQ=24-3t.
��S=36-![]() (12-t)-3(3+24-3t)
(12-t)-3(3+24-3t)
=36-18+![]() t-81+9t
t-81+9t
=![]() t-63.
t-63.
�ڵ�8![]() t
t![]() 10ʱ����ͼ2��S=�����ε����-��POD�����-��AOQ�����.
10ʱ����ͼ2��S=�����ε����-��POD�����-��AOQ�����. 
��PC=t-6,BQ=3(t-8)=3t-24,
��PD=12-t,AQ=30-3t.
��S=36-![]() (12-t)-
(12-t)-![]() (30-3t)
(30-3t)
=36-18+![]() t-45+
t-45+![]() t.
t.
=6t-27.
��10<t![]() ʱ����ͼ3. S=�����ε����-��POD�����.
ʱ����ͼ3. S=�����ε����-��POD�����.
��PC=t-6, 
��PD=12-t,
��S=36-![]() (12-t)
(12-t)
=36-18+![]() t
t
=![]() t+18.
t+18.
����������![]() ��
��![]() ������
������![]() ��������������ͼ�����
��������������ͼ�����![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
��6![]() t
t![]() ʱS=
ʱS=![]() t-63����8
t-63����8![]() t
t![]() 10ʱ��S=6t-27����10<t
10ʱ��S=6t-27����10<t![]() ʱS=
ʱS=![]() t+18.
t+18.