Question

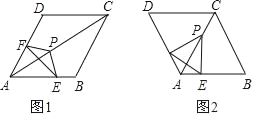
【题目】如图1，菱形ABCD中，△EFP的顶点E、F、P分别在线段AB、AD、AC上，且EP=FP．

（1）证明：∠EPF+∠BAD=180°．

（2）若∠BAD=120°（如图2），证明：AE+AF=AP．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】分析：（1）如图1中，作PM⊥AD于M，PN⊥AC于N．由Rt△PMF≌Rt△PNE，推出∠MPF=∠NPE，推出∠EPF=∠MPF，由∠BAD+∠MPN=360°-∠AMP-∠ANP=180°，推出∠EPF+∠BAD=180°即可；

（2）如图2中，作PM⊥AD于M，PN⊥AC于N．由Rt△PMF≌Rt△PNE，推出FM=NE，由PA=PA，PM=PN，推出Rt△PAM≌Rt△PAN，推出AM=AN，推出AF+AE=（AM+FM）+（AN-EN）=2AM，再证明PA=2AM即可解决问题；

详解：（1）如图1中，作PM⊥AD于M，PN⊥AC于N．

∵四边形ABCD是菱形，

∴∠PAM=∠PAN，

∴PM=PN，

∵PE=PF，

∴Rt△PMF≌Rt△PNE，

∴∠MPF=∠NPE，

∴∠EPF=∠MPF，

∵∠BAD+∠MPN=360°﹣∠AMP﹣∠ANP=180°，

∴∠EPF+∠BAD=180°．

（2）如图2中，作PM⊥AD于M，PN⊥AC于N．

由（1）可知Rt△PMF≌Rt△PNE，

∴FM=NE，

∵PA=PA，PM=PN，

∴Rt△PAM≌Rt△PAN，

∴AM=AN，

∴AF+AE=（AM+FM）+（AN﹣EN）=2AM，

∵∠BAD=120°，

∴∠PAM=60°，易知PA=2AM，

∴AE+AF=PA．