题目内容
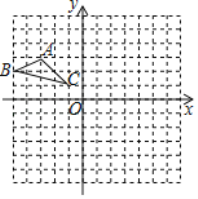
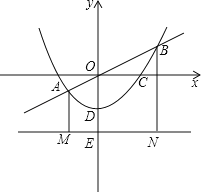
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2﹣5ax+4a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧.
(1)求点A,B的坐标;
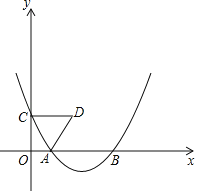
(2)当CD∥x轴时,求抛物线的函数表达式;
(3)连接BD,当BD最短时,请直接写出抛物线的函数表达式.
【答案】(1)点A、B的坐标分别为(1,0)、(4,0);(2)y=![]() x2﹣
x2﹣![]() x+
x+![]() ;(3)y=
;(3)y=![]() x2﹣
x2﹣![]() x+
x+![]() .
.
【解析】
(1)根据抛物线解析式求解与x轴的交点坐标即y=0是x的值,即可得出A,B的坐标;
(2)根据三角形ACD是等边三角形可知∠OCA的度数,根据三角函数值可求点C坐标,从而可求答案;
(3)过点D作DE⊥AC于点E,过点D作x轴的垂线于点H,过点E作EF∥x轴交y轴于点F交DH于点G,根据点E坐标进一步求△CFE∽△EGD,进而可求答案.
(1)y=ax2﹣5ax+4a,令y=0,则x=1或4,
∵点A在点B的左边
故点A、B的坐标分别为:(1,0)、(4,0);
(2)∵点A坐标为(1,0),∴OA=1
∵△ACD是等边三角形,∴∠DCA=60°
当CD∥x轴时,∠DCO=90°
∴∠ACO=30°,则∠OCA=60°,
则OC=OAtan60°=![]() ,故点C(0,
,故点C(0,![]() ),
),
即![]() =4a,解得:a=
=4a,解得:a=![]() ,
,
故抛物线的表达式为:![]() ;
;
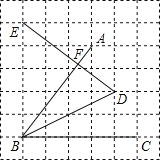
(3)如图,过点D作DE⊥AC于点E,过点D作x轴的垂线于点H,过点E作EF∥x轴交y轴于点F交DH于点G,
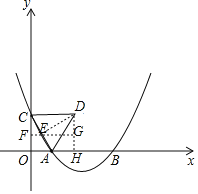
∵△ACD为等边三角形,则点E为AC的中点,则点E(![]() ,2a),AE=CE=
,2a),AE=CE=![]() ED,
ED,
∵∠CEF+∠FCE=90°,∠CEF+∠DEG=90°,∴∠DEG=∠ECF,
∴△CFE∽△EGD,∴![]() ,其中EF=
,其中EF=![]() ,CF=2a,
,CF=2a,
解得:GE=![]() a,DG=
a,DG=![]() ,故点D(
,故点D(![]() ),
),
BD2=(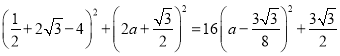 ,
,
故当a=![]() 时,BD最小,
时,BD最小,
故抛物线的表达式为:y=![]() .
.

 名校课堂系列答案
名校课堂系列答案