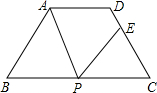
题目内容
如图,已知在梯形ABCD中,AD∥BC,∠ABC=60°,BD平分∠ABC,且BD⊥DC,CD=4.
(1)求AD的长;
(2)求梯形ABCD的面积.

(1)求AD的长;
(2)求梯形ABCD的面积.

(1)∵BD平分∠ABC,∠ABC=60°,
∴∠1=∠2=
∠ABC=30°.
又∵BD⊥DC,
∴∠C=60°.
∴∠ABC=∠C.
∴AB=CD=4.
∵AD∥BC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3.
∴AD=AB=4;
(2)过点D作DE⊥BC于点E,
在Rt△DBC中,∠1=30°,
∴BC=2CD=8.
在Rt△DEC中,∠C=60°,
∴∠4=30°.
∴EC=
CD=2.
∴DE=
=2
,
∴S梯形ABCD=
(AD+BC)•DE=12
.

∴∠1=∠2=
| 1 |
| 2 |
又∵BD⊥DC,
∴∠C=60°.
∴∠ABC=∠C.
∴AB=CD=4.
∵AD∥BC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3.
∴AD=AB=4;
(2)过点D作DE⊥BC于点E,
在Rt△DBC中,∠1=30°,
∴BC=2CD=8.
在Rt△DEC中,∠C=60°,
∴∠4=30°.
∴EC=
| 1 |
| 2 |
∴DE=
| CD2-EC2 |
| 3 |
∴S梯形ABCD=
| 1 |
| 2 |
| 3 |


练习册系列答案
相关题目