题目内容
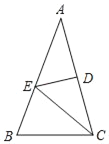
【题目】如图,在△ABC中,∠ABC=90°,AB=BC, BD⊥AC,垂足为D,过点D作DE⊥DF,交AB于点E,交BC于点F.

(1)求证:△DBE≌△DCF;
(2)连接EF,若AE=4,FC=3;求
①EF的长;
②四边形BFDE的面积.
【答案】(1)见解析;(2)①5;②12![]()
【解析】
(1)根据的等腰直角三角形的性质以及“ASA”证明△BED≌△CFD即可;
(2)①根据全等得出AE=BF、BE=CF,由AE=BF,FC=BE就可以求得EF的长;
②根据勾股定理求出DE、DF长,根据三角形的面积公式求出即可.
(1)证明:∵D是AC中点,
∴∠ABD=∠CBD=45°,BD=AD=CD,BD⊥AC,
∵∠EDB+∠FDB=90°,∠FDB+∠CDF=90°,
∴∠EDB=∠CDF,
在△BED和△CFD中,
∵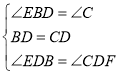 ,
,
∴△BED≌△CFD;
(2)解:①∵△BED≌△CFD,
∴BE=CF=3;
同理可证:△AED≌△BFD,
∴AE=BF=4,
∵AB=BC,BE=CF=3,
∴AE=BF=4,
在Rt△BEF中,EF=![]() =5;
=5;
②∵△BED≌△CFD,
∴DE=DF,
∵∠EDF=90°,EF=5,
∴2DE2=52,
∴DE=DF=![]() ,
,
∵BE=3,BF=4,∠ABC=90°,
∴四边形BFDE的面积S=S△EBF+S△EDF=![]() ×
×![]() ×
×![]() =6+
=6+![]() =12
=12![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目