题目内容
【题目】已知:如图,在△ABC中,AB=AC, BD、CE是高,BD与CE相交于点O,

求证:(1)OB=OC;
(2)点O在∠BAC的角平分线上.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AAS可证△BEC≌△CDB,利用全等三角形的性质得△BEC≌△CDB,从而可证OB=OC;
(2)作直线AO.由AB=AC,OB=OC,推出OA垂直平分线段BC,利用等腰三角形的性质即可解决问题;
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°,
∴△BEC≌△CDB,
∴∠BCE=∠CBD,
∴OB=OC;
(2)证明:作直线AO.
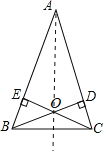
∵AB=AC,OB=OC,
∴OA垂直平分线段BC,
∵AB=AC,
∴OA平分∠BAC,
∴点O在∠BAC的平分线上.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目