Question

【题目】如图1，△ABC是边长为8的等边三角形，AD⊥BC于点D，DE⊥AB于点E.

（1）求证：AE＝3EB

（2）若点F是AD的中点，点P是BC边上的动点，连接PE，PF，如图2所示，求PE＋PF的最小值及此时BP的长；

（3）在（2）的条件下，连接EF，当PE＋PF取最小值时，△PEF的面积是______.

Answer 1

【答案】（1）见解析；（2）PE＋PF的最小值是6，此时BP的长为2；（3）.

【解析】

（1）在三角形BED和三角形ABD中证明即可；

（2）作点F关于BC的对称点点G，连接EG交BC于点P，此时PE＋PF的值最小等于EG.

作EH⊥AD于H，在直角三角形EGH中求出EG的长即可；可证明△EBP是等边三角形，即可求出BP的长；

（3）证明三角形PEF是直角三角形即可求出面积.

解：（1）如图1，

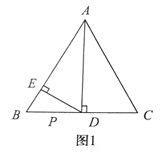
∵△ABC是等边三角形，

∴∠B=，

∵AD⊥BC，DE⊥AB，

∴∠BDE=，∠BAD=，

∴

∴AB=4BE，

∴AE=3BE；

（2）如图2，作点F关于BC的对称点点G，连接EG交BC于点P，此时PE＋PF的值最小，

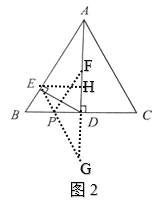
作EH⊥AD于H，

由（1）可知AE=6，∠EAH=，

∴EH=3，AH=，

∵AB=8，∠BAD=，

∴BD=4，AD=，

∴DG=DF=，DH=，

∴GH=，

∴，

∴PE+PF=PE+PG=EG=6，

∴EG=AE，

∴∠G=∠EAH=，

∴∠DPG=，

∴∠EPB=，

∴∠EPB=∠B=，

∴△EBP是等边三角形，

∴BP=BE=2；

∴PE＋PF的最小值是6，此时BP的长为2.

（3）如图2，连接EF，

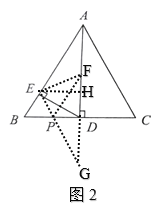
在直角三角形AED中，EF是AD边上的中线，

∴EF=FD=，

∵∠ADE=，

∴△EDF是等边三角形，

∴∠DEF=，

由（2）可知∠BEP=，

∴∠DEP=，

∴∠PEF=，

∴S△PEF==.