Question

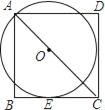
【题目】如图，O为正方形ABCD对角线上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E．

（1）求证：CD是⊙O的切线；

（2）若正方形ABCD的边长为10，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）⊙O的半径为：20﹣10．

【解析】分析：（1）首先连接OE，并过点O作OF⊥CD，由OA长为半径的⊙O与BC相切于点E，可得OE=OA，OE⊥BC，然后由AC为正方形ABCD的对角线，根据角平分线的性质，可证得OF=OE=OA，即可判定CD是⊙O的切线；

（2）由正方形ABCD的边长为10，可求得其对角线的长，然后由设OA=r，可得OE=EC=r，由勾股定理求得OC=r，则可得方程r+r=10，继而求得答案．

详解：（1）连接OE，并过点O作OF⊥CD．

∵BC切⊙O于点E，∴OE⊥BC，OE=OA．

又∵AC为正方形ABCD的对角线，∴∠ACB=∠ACD，∴OF=OE=OA，即：CD是⊙O的切线．

（2）∵正方形ABCD的边长为10，∴AB=BC=10，∠B=90°，∠ACB=45°，∴AC==10．

∵OE⊥BC，∴OE=EC，设OA=r，则OE=EC=r，∴OC==r．

∵OA+OC=AC，∴r+r=10，解得：r=20﹣10，∴⊙O的半径为：20﹣10．