Question

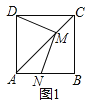
【题目】已知，在平行四边形ABCD中，E为AD上一点，且AB=AE，连接BE交AC于点H，过点A作AF⊥BC于F，交BE于点G.

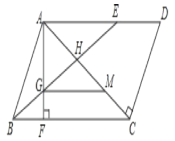
(1)若∠D=50°，求∠EBC的度数；

(2)若AC⊥CD,过点G作GM∥BC交AC于点M，求证：AH=MC.

Answer 1

【答案】（1）∠EBC=25°；（2）见解析；

【解析】

（1）根据等边对等角以及平行线的性质，即可得到∠1=∠2=∠ABC，再根据平行四边形ABCD中，∠D=50°=∠ABC，可得出∠EBC的度数；

（2）过M作MN⊥BC于N，过G作GP⊥AB于P，则∠CNM=∠APG=90°，先根据AAS判定△BPG≌△BFG，得到PG=GF，根据矩形GFNM中GF=MN，即可得出PG=NM，进而判定△PAG≌△NCM（AAS），可得AG=CM，再根据等角对等边得到AH=AG，即可得到结论．

(1)∵AB=AE，

∴∠1=∠3，

∵AE∥BC，

∴∠2=∠3，

∴∠1=∠2=∠ABC，

又∵平行四边形ABCD中,∠D=50°，

∴∠ABC=50°，

∴∠EBC=25°；

(2)证明：如图,过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°，

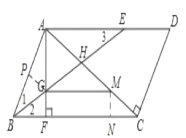
由(1)可得，∠1=∠2，

∵AF⊥BC，

∴∠BPG=∠BFG=90°，

在△BPG和△BFG中，

，

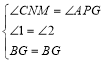∴△BPG≌△BFG(AAS)，

∴PG=GF，

又∵矩形GFNM中，GF=MN，

∴PG=NM，

∵AC⊥CD,CD∥AB，

∴∠BAC=90°=∠AFB，

即∠PAG+∠ABF=∠NCM+∠ABC=90°，

∴∠PAG=∠NCM，

在△PAG和△NCM中，

，

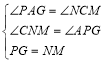∴△PAG≌△NCM(AAS)，

∴AG=CM，

∵∠1=∠2，∠BAH=∠BFG，

∴∠AHG=∠FGB=∠AGH，

∴AG=AH，

∴AH=MC.