题目内容
【题目】在△ABC中，∠C=90°，∠BAC=60°，△ABC绕点C顺时针旋转，旋转角为α（0°＜α＜180°），点A、B的对应点分别是点D、E．
（1）如图1，当点D恰好落在边AB上时，试判断DE与AC的位置关系，并说明理由．
（2）如图2，当点B、D、E三点恰好在一直线上时，旋转角α=__°，此时直线CE与AB的位置关系是__．
（3）在（2）的条件下，联结AE，设△BDC的面积S1，△AEC的面积S2，则S1与S2的数量关系是_____．
（4）如图3，当点B、D、E三点不在一直线上时，（3）中的S1与S2的数量关系仍然成立吗？试说明理由．
【答案】 （1）DE∥AC (2) 120° EC⊥AB． S1=S2） (4) S1=S2仍然成立
【解析】试题分析：
（1）由旋转的性质可得∠EDC=∠BAC，DC=AC结合∠BAC=60°，可得△ADC是等边三角形，从而可得∠DCA=∠EDC=60°，由此可得DE∥AC；
（2）如下图2，在△ABC中，由∠C=90°，∠BAC=60°可得∠ABC=30°，延长EC交AB于点F，由旋转的性质可得CE=BE，∠E=∠ABC=30°，结合B、D、E的三点在同一直线上可得∠CBE=∠E=30°，从而可得旋转角∠BCE=120°，结合∠BCE=∠ABC+∠BFC，∠ABC=30°，可得∠BFC=90°，从而可得EC⊥AB；
（3）如上图2，过点D作DH⊥BC于点H，由∠DCF=∠ACB=90°易得∠ACF=∠DCH，结合∠AFC=∠DHC=90°，AC=DC可得△ACF≌△DCH，从而可得AF=DH，结合BC=EC即可得到S1=S2；
（4）如下图3，过D作DH⊥BC于H，过A作AG⊥EC交EC的延长线于G，与（3）同理可得△AGC≌△DHC，从而可得AG=HD，结合EC=BC即可得到S1=S2仍然成立.
试题解析：
（1）DE∥AC．理由：∵△ABC旋转后与△DCE全等，
∴∠A=∠CDE，AC=DC．
∵∠BAC=60°，AC=DC，
∴△DAC是等边三角形．
∴∠DCA=60°．
又∵∠CDE=∠BAC=60°，
∴∠DCA=∠CDE=60°，
∴DE∥AC．
（2）120°；EC⊥AB，理由如下：
如下图2，延长EC交AB于点F，
∵在△ABC中，由∠C=90°，∠BAC=60°，
∴∠ABC=30°，
由旋转的性质可得：CE=BE，∠E=∠ABC=30°，
∵B、D、E的三点在同一直线上，
∴∠CBE=∠E=30°，
∴旋转角∠BCE=120°，
又∵∠BCE=∠ABC+∠BFC，∠ABC=30°，
∴∠BFC=120°-30°=90°，
∴EC⊥AB于点F；
（3）S1=S2，理由如下：
如上图2，连接AE，过点D作DH⊥BC于点H，
∴∠AFC=∠DHC=90°，
∵∠ACB=∠DCE=90°，
∴∠ACF=∠DCH，
又∵AC=DC，
∴△ACF≌△DCH，
∴AF=DH，
又∵EC=BC，
∴
CE·AF=BC·DH，即S1=S2；
（4）S1=S2仍然成立，理由如下：
如下图3所示：过D作DH⊥BC于H，过A作AG⊥EC交EC的延长线于G．
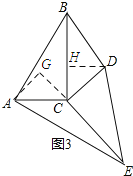
∵DH⊥BC，AG⊥EC，
∴∠AGC=∠DHC=90°
∵△ABC旋转后与△DCE全等
∴∠ACB=∠DCE=90°，AC=DC，BC=CE．
∵∠ACE+∠BCD=180°，∠GCA+∠ECA=180°，
∴∠ACG=∠DCH，
又∵∠AGC=∠DHC，AC=DC，
∴△AGC≌△DHC，
∴AG=DH，
∴ECAF=CBDG，即S1=S2．
