题目内容
【题目】阅读下列材料，并按要求解答．
（模型建立）如图①，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．求证：△BEC≌△CDA．
（模型应用）
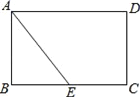
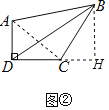
应用1：如图②，在四边形ABCD中，∠ADC＝90°，AD＝6，CD＝8，BC＝10，AB2＝200．求线段BD的长．
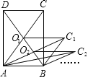
应用2：如图 ③，在平面直角坐标系中，纸片△OPQ为等腰直角三角形，QO＝QP，P（4，m），点Q始终在直线OP的上方．
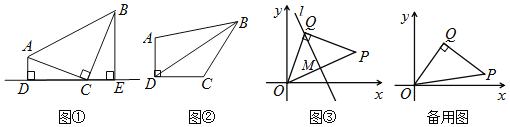
（1）折叠纸片，使得点P与点O重合，折痕所在的直线l过点Q且与线段OP交于点M，当m＝2时，求Q点的坐标和直线l与x轴的交点坐标；
（2）若无论m取何值，点Q总在某条确定的直线上，请直接写出这条直线的解析式 ．
【答案】模型建立：见解析；应用1：2
；应用2：（1）Q(1，3)，交点坐标为(
，0)；（2）y＝﹣x+4
【解析】
根据AAS证明△BEC≌△CDA，即可；
应用1：连接AC，过点B作BH⊥DC，交DC的延长线于点H，易证△ADC≌△CHB，结合勾股定理，即可求解；
应用2：（1）过点P作PN⊥x轴于点N，过点Q作QK⊥y轴于点K，直线KQ和直线NP相交于点H，易得：△OKQ≌△QHP，设H(4，y)，列出方程，求出y的值，进而求出Q(1，3)，再根据中点坐标公式，得P(4，2)，即可得到直线l的函数解析式，进而求出直线l与x轴的交点坐标；（2）设Q(x，y)，由△OKQ≌△QHP，KQ＝x，OK＝HQ＝y，可得：y＝﹣x+4，进而即可得到结论．
如图①，∵AD⊥ED，BE⊥ED，∠ACB＝90°，
∴∠ADC＝∠BEC＝90°，
∴∠ACD+∠DAC＝∠ACD+∠BCE＝90°，
∴∠DAC＝∠BCE，
∵AC＝BC，
∴△BEC≌△CDA（AAS）；
应用1：如图②，连接AC，过点B作BH⊥DC，交DC的延长线于点H，
∵∠ADC＝90°，AD＝6，CD＝8，
∴AC＝10，
∵BC＝10，AB2＝200，
∴AC2+BC2＝AB2，
∴∠ACB＝90°，
∵∠ADC＝∠BHC＝∠ACB＝90°，
∴∠ACD＝∠CBH，
∵AC＝BC＝10，
∴△ADC≌△CHB（AAS），
∴CH＝AD＝6，BH＝CD＝8，
∴DH=6+8=14，
∵BH⊥DC，
∴BD＝
＝2；
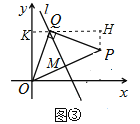
应用2：（1）如图③，过点P作PN⊥x轴于点N，过点Q作QK⊥y轴于点K，直线KQ和直线NP相交于点H，
由题意易：△OKQ≌△QHP（AAS），
设H(4，y)，那么KQ＝PH＝y﹣m＝y﹣2，OK＝QH＝4﹣KQ＝6﹣y，
又∵OK＝y，
∴6﹣y＝y，y＝3，
∴Q(1，3)，
∵折叠纸片，使得点P与点O重合，折痕所在的直线l过点Q且与线段OP交于点M，
∴点M是OP的中点，
∵P(4，2)，
∴M(2，1)，
设直线Q M的函数表达式为：y＝kx+b，
把Q(1，3)，M(2，1)，代入上式得：
，解得：
∴直线l的函数表达式为：y＝﹣2x+5，
∴该直线l与x轴的交点坐标为(，0)；
（2）∵△OKQ≌△QHP，
∴QK＝PH，OK＝HQ，
设Q(x，y)，
∴KQ＝x，OK＝HQ＝y，
∴x+y＝KQ+HQ＝4，
∴y＝﹣x+4，
∴无论m取何值，点Q总在某条确定的直线上，这条直线的解析式为：y＝﹣x+4，
故答案为：y＝﹣x+4．
