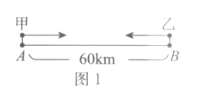
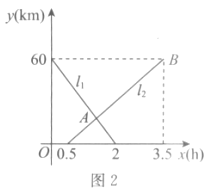
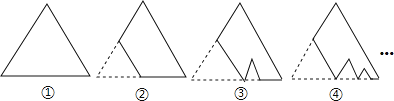
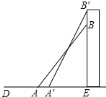
题目内容
【题目】已知抛物线 y=a（x﹣2）
+1 经过点 P（1，﹣3）
(1)求 a 的值；
(2)若点 A（m，y
）、B（n ，y
）（m＜n＜2）都在该抛物线上，试比较 y与y的大小．
【答案】（1）a=﹣4．（2）y1＜y2．
【解析】
（1）将点（1，﹣3）代入y=a（x﹣2）2+1，运用待定系数法即可求出a的值。；
（2）先求得抛物线的对称轴为x=2，再判断A（m，y1）、B（n，y2）（m＜n＜3）在对称轴左侧，从而判断出y1与y2的大小关系。
解：（1）∵抛物线过点 P（1，﹣3），
∴﹣3=a+1，解得 a=﹣4．
（2）当 a=﹣4 时，抛物线的解析式为 y=﹣4（x﹣2）2+1．
∴抛物线的开口向下，对称轴为 x=2，
∴当 x≤2 时，y 随 x 的增大而增大，
∵m＜n＜2，
∴y1＜y2．
练习册系列答案
53随堂测系列答案
相关题目
