题目内容
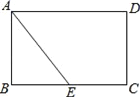
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
【答案】![]()
【解析】如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.首先求得AE=5.然后在求得OE=![]() .,OB=
.,OB=![]() ,由翻折的性质可知BB′=
,由翻折的性质可知BB′=![]() ,接下来证明△BOE∽△BFB′,由相似三角形的性质可得到:
,接下来证明△BOE∽△BFB′,由相似三角形的性质可得到:![]() ,
,![]() ,从而可求得FC=
,从而可求得FC=![]() ,Rt△B′FC中,由勾股定理可求得B′C=
,Rt△B′FC中,由勾股定理可求得B′C=![]() .
.
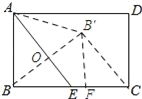
解:如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.
∵点E是BC的中点,
∴BE=![]() .
.
在Rt△ABE中,AE=![]() .
.
由射影定理可知;OEAE=BE2,
∴OE=![]() .
.
由翻折的性质可知;BO⊥AE.
∴![]() .
.
∴OB=![]() .
.
∴BB′=![]() .
.
∵∠OBE=∠FBB′,∠BOE=∠BFB′,
∴△BOE∽△BFB′.
∴![]() =
=![]() ,即
,即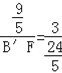 =
=![]() .
.
解得:![]() ,
,![]() .
.
∴FC=![]() .
.
在Rt△B′FC中,B′C=![]() =
=![]() .
.
故答案为:![]() .
.
“点睛”本题主要考查的是翻折的性质、勾股定理、相似三角形的性质和判定,求得B′F、BF的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】雾霾已经成为时下最普遍与敏感的话题.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
级别 | 观 点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |

请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.