题目内容
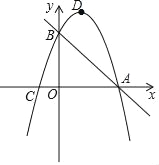
【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点M的坐标为(0、3)或2,3)或(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3);(3)点N的坐标为(1,0)或(﹣7,0).
,﹣3);(3)点N的坐标为(1,0)或(﹣7,0).
【解析】试题分析:(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求得b,c的值即可;
(2)设M的坐标为(x,y),由△ACM与△ABC的面积相等可得到|y|=3,将y=3或y=-3代入抛物线的解析式求得对应的x的值,从而得到点M的坐标;
(3)先利用配方法求得点D的坐标,当∠DNA=90°时,DN⊥OA,可得到点N的坐标,从而得到AN=2,然后再求得AD的长;当∠N′DA=90°时,依据sin∠DN′A=sin∠ADN可求得AN′的长,从而可得到N′的解析式.
试题解析:(1)将x=0代入AB的解析式得:y=3,
∴B(0,3).
将y=0代入AB的解析式得:﹣x+3=0,解得x=3,
A(3,0).
将点A和点B的坐标代入得: ![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)设M的坐标为(x,y).
∵△ACM与△ABC的面积相等,
∴![]() AC|y|=
AC|y|=![]() ACOB.
ACOB.
∴|y|=OB=3.
当y=3时,﹣x2+2x+3=3,解得x=0或x=2,
∴M(2,3)、(0、3).
当y=﹣3时,﹣x2+2x+3=3,解得:x=1+![]() 或x=1﹣
或x=1﹣![]() .
.
∴M(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3).
,﹣3).
综上所述点M的坐标为(0、3)或2,3)或(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3).
,﹣3).
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
①当∠DNA=90°时,如图所示:
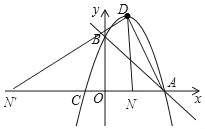
∵∠DNA=90°时,
∴DN⊥OA.
又∵D(1,4)
∴N(1,0).
∴AN=2.
DN=4,AN=2,
∴AD=2![]() .
.
②当∠N′DA=90°时,则DN′A=∠NDA.
∴![]() ,即
,即![]() ,解得:AN′=10.
,解得:AN′=10.
∵A(3,0),
∴N′(﹣7,0).
综上所述点N的坐标为(1,0)或(﹣7,0).