Question

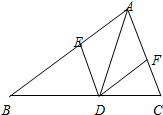15、如图，已知AD是△ABC的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是：

AE=AF或∠EDA=∠FDA

．

Answer 1

分析：要证两三角形全等的判定，已经有∠EAD=∠FAD，AD=AD，所以再添加一对边或一对角相等即可得证．

解答：解：①添加条件：AE=AF，
证明：在△AED与△AFD中，
∵AE=AF，∠EAD=∠FAD，AD=AD，
∴△AED≌△AFD（SAS），
②添加条件：∠EDA=∠FDA，
证明：在△AED与△AFD中，
∵∠EAD=∠FAD，AD=AD，∠EDA=∠FDA，
∴△AED≌△AFD（ASA）．
故答案为：AE=AF或∠EDA=∠FDA．

点评：本题是开放性题目，主要考查三角形全等的判定方法，只要符合题意即可．
全等三角形的判定方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．