题目内容
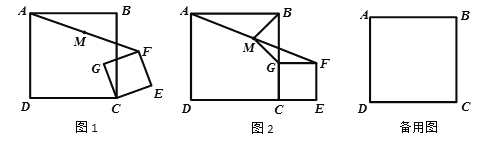
【题目】如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且AF=FC,GH⊥CD于H.下列说法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,则∠EGH=40°.其中正确的有________.

【答案】①②③④.
【解析】
灵活利用平行线的性质、等角的余角相等、四边形的内角和、三角形内角和定理、三角形的面积公式、角平分线的性质进行分析.
解:①中,根据两条直线平行,同旁内角互补,得∠BAC+∠ACD=180°,
再根据角平分线的概念,得∠GAC+∠GCA=![]() ∠BAC+
∠BAC+![]() ∠ACD=
∠ACD=![]() ×180°=90°,
×180°=90°,
再根据三角形的内角和是180°,得AG⊥CG;
②中,根据等角的余角相等,得∠CGE=∠GAC,故∠BAG=∠CGE;
③中,根据三角形的面积公式,
∵AF=CF,∴S△AFG=S△CFG;
④中,根据题意得:在四边形GECH中,∠EGH+∠ECH=180°.
又∠EGH:∠ECH=2:7,则∠EGH=180°×![]() =40°.
=40°.
故上述四个都是正确的.
故答案为:①②③④.

练习册系列答案
相关题目