题目内容
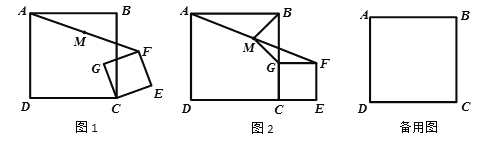
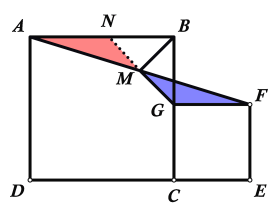
【题目】如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)DG=
;(3)DG=![]() MG,理由见解析.
MG,理由见解析.
【解析】
(1)连接MG并延长交AB于N点,证明△ANM≌△FGM后得到MG=MN,AN=CG,进而得到BN=BG,得到△ANG为等腰直角三角形,即可证明MG=MB.
(2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.
(3)先画出图形,然后证明△ADG≌△ABG,得到DG=BG,又△BMG为等腰直角三角形,故而得到DG=BG=![]() MG.
MG.
解:(1) 连接MG并延长交AB于N点,如下图所示:
∵GF∥AN,
∴∠NAM=∠GFM
在△ANM和△FGM中
 ,∴△ANM≌△FGM(ASA)
,∴△ANM≌△FGM(ASA)
∴MG=MN,CG=GF=AN
∴AB-AN=BC-CG
∴NB=GB
∴△NBG为等腰直角三角形
又M是NG的中点
∴由直角三角形斜边上的中线等于斜边的一半知:
故有:MG=MB.
(2)分类讨论:
情况一:当B、G、F三点在正方形ABCD外同一直线上时

延长MG到N点,并使得MG=MN,连接AN,BN
∴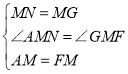 ,∴△AMN≌△FMG(SAS)
,∴△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB+∠ABG=180°
又∠ABC=90°
∴∠NAB+∠CBG=90°
又在△BCG中,∠BCG+∠CBG=90°
∴∠NAB=∠BCG
∴在△ABN中和△CBG中: ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在Rt△BCG中,![]()
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
在Rt△MFH中,![]()
情况二:当B、G、F三点在正方形ABCD内同一直线上时
如下图所示,延长MG到MN,并使得MG=MN,连接NA、NB,
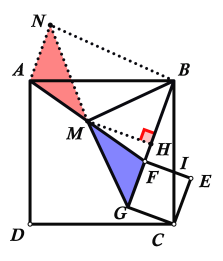
同情况一中证明思路,
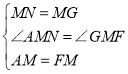 ,△AMN≌△FMG(SAS)
,△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB=∠ABG
又∠ABG+∠GBC=90°
∠GBC+∠BIF=90°
∴∠BIF=∠ABG
又∠BIF=∠BCG,∠ABC=∠NAB
∴∠NAB=∠GCB
∴在△ABN中和△CBG中: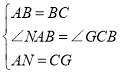 ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在△BCG中,![]()
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
∴HF=HG-GF=2-1=1
在Rt△MFH中,![]()
故答案为:![]() 或
或![]()
(3)由题意作出图形如下所示:
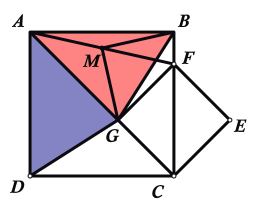
DG、MG的数量关系为:DG=![]() MG,理由如下:
MG,理由如下:
∵G点在AC上
∴∠DAG=∠BAG=45°
在△ADG和△ABG中:
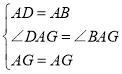 ,∴△ADG≌△BAG(SAS)
,∴△ADG≌△BAG(SAS)
∴DG=BG
又由(2)中的证明过程可知:△MBG为等腰直角三角形
∴BG=![]() MG
MG
∴DG=![]() MG
MG
故答案为:DG=![]() MG.
MG.

 优学名师名题系列答案
优学名师名题系列答案