Question

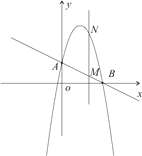
【题目】如图，一次函数分别交y轴、x 轴于A、B两点，抛物线过A、B两点。（1）求这个抛物线的解析式；（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N。求当t 取何值时，MN有最大值？最大值是多少？

Answer 1

【答案】（1）；

（2） 当t=2时，MN的最大值是4.

【解析】试题分析：（1）求出点A、点B的坐标，将A、B坐标代入抛物线解析式，求出b、c的值即可；（2）将M、N的坐标用含t的式子表示，然后将MN表示为二次函数的形式，求二次函数最值即可.

试题解析：

（1）易得A（0，2），B（4，0），

将x=0，y=2代入y=－x2+bx+c得c=2，

将x=4，y=0 代入y=－x2+bx+2，得－16+4b+2=0，解得b=，

∴抛物线解析式为y=－x2+x+2；

（2）由题意易得M(t，－ t+2)，N(t，－t2+t+2)，

∴MN=－t2+t+2－（－t+2）=－t2+t+2+t－2=－t2+4t=－（t－2）2+4，

∴当t=2时，MN有最大值4.